about fast slow points 1
my fast slow point leet code list leetcode
- Linked List Cycle 141
- Linked List Cycle II 142
- Happy Number 202
- Reorder List 143
- Remove Duplicates from Sorted Array 26
- Find the Duplicate Number 287
- Maximum Twin Sum of a Linked Li
- Delete the Middle Node of a Linked Lis
- Convert Sorted List to Binary Search Tree 109
- Car Fleet II 1776
Linked List Cycle 141
Given head, the head of a linked list, determine if the linked list has a cycle in it.
There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the next pointer. Internally, pos is used to denote the index of the node that tail's next pointer is connected to. Note that pos is not passed as a parameter.
Return true if there is a cycle in the linked list. Otherwise, return false.
Input: head = [3,2,0,-4], pos = 1
Output: true
Explanation: There is a cycle in the linked list, where the tail connects to the 1st node (0-indexed).
wrong answer, fast, slow at the head position
public boolean hasCycle(ListNode head) {
ListNode fast = head;
ListNode slow = head;
while (fast != null && fast.next != null) {
if (fast == slow) {
return true;
}
fast = fast.next.next;
slow = slow.next;
}
return false;
}
不用去判断 corner case, 都包含了
public boolean hasCycle(ListNode head) {
ListNode fast = head, slow = head;
while (fast != null && fast.next != null) {
fast = fast.next.next;
slow = slow.next;
if (slow == fast) {
return true;
}
}
return false;
}
Linked List Cycle II 142
Given the head of a linked list, return the node where the cycle begins. If there is no cycle, return null.
There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the next pointer. Internally, pos is used to denote the index of the node that tail's next pointer is connected to (0-indexed). It is -1 if there is no cycle. Note that pos is not passed as a parameter.
Do not modify the linked list.
Input: head = [3,2,0,-4], pos = 1
Output: tail connects to node index 1
Explanation: There is a cycle in the linked list, where tail connects to the second node.
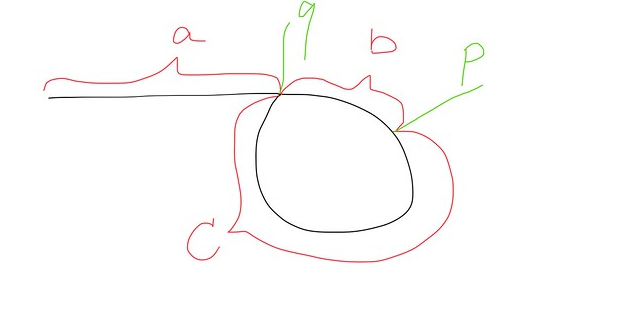
fast slow points
ListNode slow = head, fast = head;
while (fast != null && fast.next != null) {
fast = fast.next.next;
slow = slow.next;
if (fast == slow) {
slow = head;
while (fast != slow) {
fast = fast.next;
slow = slow.next;
}
return slow;
}
}
return null;
}
Happy Number 202
Write an algorithm to determine if a number n is happy.
A happy number is a number defined by the following process:
Starting with any positive integer, replace the number by the sum of the squares of its digits.
Repeat the process until the number equals 1 (where it will stay), or it loops endlessly in a cycle which does not include 1.
Those numbers for which this process ends in 1 are happy.
Return true if n is a happy number, and false if not.
Example 1:
Input: n = 19
Output: true
Explanation:
12 + 92 = 82
82 + 22 = 68
62 + 82 = 100
12 + 02 + 02 = 1
statement that if a number ain’t happy then it will lead to a cycle … and whenever you hear the word cycle the first thing you should remember is “Floyd’s cycle-finding algorithm” also known as “Tortoise and the Hare algorithm”
快慢指针
public boolean isHappy(int n) {
int s = n,f = n; // slow , fast
do{
s = compute(s); // slow computes only once
f = compute(compute(f)); // fast computes 2 times
if(s == 1)return true; // if we found 1 then happy indeed !!!
}while(s != f); // else at some point they will meet in the cycle
return false; // it's a cycle , not happy at all !!!
}
public int compute(int n){
int s = 0;
while(n != 0){
s += (n%10)*(n%10);
n = n/10;
}
return s;
}
Reorder List 143
You are given the head of a singly linked-list. The list can be represented as:
L0 → L1 → … → Ln - 1 → Ln
Reorder the list to be on the following form:
L0 → Ln → L1 → Ln - 1 → L2 → Ln - 2 → …
You may not modify the values in the list's nodes. Only nodes themselves may be changed.
Input: head = [1,2,3,4]
Output: [1,4,2,3]
split into two halves, merge
public void reorderList(ListNode head) {
ListNode midNode = midNode(head);
ListNode newNode = reverse(midNode.next);
midNode.next = null;
ListNode cur1 = head, cur2 = newNode, cur = null;
while (cur1 != null && cur2 != null) {
cur = cur1.next;
cur1.next = cur2;
cur1 = cur2;
cur2 = cur;
}
}
ListNode midNode(ListNode head){
ListNode fast = head, slow = head;
while(fast.next!=null && fast.next.next!=null){
fast = fast.next.next;
slow = slow.next;
}
return slow;
}
ListNode reverse(ListNode head) {
ListNode curr = head, prev= null, next = null;
while(curr!=null){
next = curr.next;
curr.next = prev ;
prev = curr;
curr = next;
}
return prev;
}
TIME COMPLEXITY : O(n)
SPACE COMPLEXITY : O(1)
Single traversal leetcode solution

fast slow points
1 -> 2 -> 3 -> 4 -> 5 -> 6 left right
1 -> 6 -> 2 -> 3 -> 4 -> 5 left right
recursion call
错误的回溯
public void reorderList(ListNode head) {
ListNode cur = head;
reorder(cur, head);
}
void reorder(ListNode cur, ListNode head) {
if (head == null) {
return;
}
reorder(cur, head.next);
if (cur.next != null) {
ListNode next = cur.next;
cur.next = head;
head.next = next;
cur = next;
}
if (cur != null && cur.next == head) {
cur.next = null;
}
}
}
1 -> 2 -> 3 -> 4 cur head next cur.next = 4
新循环 cur 又是 1
这跟传参有关,所以每次都是从 1 开始, 但是弄成全局模式,就是下面讨巧的方法就可以
1 -> 2 -> 3 -> 4 cur head
所以报错说有环,因为 cur 这个值无法储存
用一个 ListNode[] 储存
public void reorderList(ListNode head) {
ListNode[] cur = new ListNode[1];
cur[0] = head;
reorder(cur, head);
}
void reorder(ListNode[] cur, ListNode head) {
if (head == null) {
return;
}
reorder(cur, head.next);
if (cur[0].next != null) {
ListNode next = cur[0].next;
cur[0].next = head;
head.next = next;
cur[0] = next;
}
if (cur != null && cur[0].next == head) {
cur[0].next = null;
}
}
}
非常讨巧的方法 leetcode
private ListNode temp;
private boolean isStop;
public void reorderList(ListNode head) {
temp = head;
isStop = false;
reorder(head);
}
private void reorder(ListNode head) {
if (head == null) return;
reorder(head.next);
if (!isStop) {
ListNode next = temp.next;
temp.next = head;
head.next = next;
temp = next;
}
if (temp != null && temp.next == head) {
temp.next = null;
isStop = true;
}
}
Remove Duplicates from Sorted Array 26
Given an integer array nums sorted in non-decreasing order, remove the duplicates in-place such that each unique element appears only once. The relative order of the elements should be kept the same.
Since it is impossible to change the length of the array in some languages, you must instead have the result be placed in the first part of the array nums. More formally, if there are k elements after removing the duplicates, then the first k elements of nums should hold the final result. It does not matter what you leave beyond the first k elements.
Return k after placing the final result in the first k slots of nums.
Do not allocate extra space for another array. You must do this by modifying the input array in-place with O(1) extra memory.
Custom Judge:
The judge will test your solution with the following code:
int[] nums = [...]; // Input array
int[] expectedNums = [...]; // The expected answer with correct length
public int removeDuplicates(int[] nums) {
int j = 1;
int i = 0;
while (j < nums.length) {
if (nums[j] != nums[j - 1]) {
nums[++i] = nums[j];
}
j++;
}
return i + 1;
}
Find the Duplicate Number 287
Given an array of integers nums containing n + 1 integers where each integer is in the range [1, n] inclusive.
There is only one repeated number in nums, return this repeated number.
You must solve the problem without modifying the array nums and uses only constant extra space.
Example 1:
Input: nums = [1,3,4,2,2]
Output: 2
其核心思想快慢指针在之前的题目 Linked List Cycle II 中就有应用,这里应用的更加巧妙一些,由于题目限定了区间 [1,n],所以可以巧妙的利用坐标和数值之间相互转换,而由于重复数字的存在,那么一定会形成环,用快慢指针可以找到环并确定环的起始位置
public int findDuplicate(int[] nums) {
if(nums.length ==0 )
return 0;
int slow=0, fast=0;
slow = nums[slow];
fast = nums[nums[fast]];
while(slow != fast){
if(slow == nums[slow])
return slow;
slow = nums[slow];
fast = nums[nums[fast]];
}
fast = 0;
while(slow != fast){
if(slow == nums[slow])
return slow;
slow = nums[slow];
fast = nums[fast];
}
return slow;
}
Bit Manipulation, 对于 int 32 位,统计 nums[0..n-1]在第 k 位的 1 的总数 b,与 0..n-1 在第 k 位的 1 的总数 a 如果 b > a,说明第 k 位存在重复(多了 1)
int findDuplicate(vector<int>& nums) {
int res = 0;
for(int k = 0; k < 32; ++k){
int bit = (1 << k); // 1 右移 k 位
int a = 0, b = 0;
for(int i = 0; i < nums.size(); ++i){
if((i & bit) > 0) ++a;
if((nums[i] & bit) > 0) ++b;
}
if(b > a) res += bit; // 重复数的k位
}
return res;
}
Maximum Twin Sum of a Linked L
In a linked list of size n, where n is even, the ith node (0-indexed) of the linked list is known as the twin of the (n-1-i)th node, if 0 <= i <= (n / 2) - 1.
For example, if n = 4, then node 0 is the twin of node 3, and node 1 is the twin of node 2. These are the only nodes with twins for n = 4.
The twin sum is defined as the sum of a node and its twin.
Given the head of a linked list with even length, return the maximum twin sum of the linked list.
Input: head = [5,4,2,1]
Output: 6
Explanation:
Nodes 0 and 1 are the twins of nodes 3 and 2, respectively. All have twin sum = 6.
There are no other nodes with twins in the linked list.
Thus, the maximum twin sum of the linked list is 6.
public int pairSum(ListNode head) {
if (head == null) {
return 0;
}
if (head.next == null) {
return head.val;
}
ListNode slow = head;
ListNode fast = head;
while (fast != null && fast.next != null) {
slow = slow.next;
fast = fast.next.next;
}
slow = reverse(slow);
fast = head;
int sum = Integer.MIN_VALUE;
while (slow != null) {
sum = Math.max(slow.val + fast.val, sum);
slow = slow.next;
fast = fast.next;
}
return sum;
}
public ListNode reverse(ListNode node) {
if (node == null) {
return null;
}
ListNode current = node;
ListNode previous = null;
while (current != null) {
ListNode next = current.next;
current.next = previous;
previous = current;
current = next;
}
return previous;
}
又是回溯,利用 head 到了尾部 null 的时候,倒退的原理
public int pairSum(ListNode head) {
ListNode prev = null;
int maxSum = 0;
public int pairSum(ListNode head) {
prev = head;
maxSum = 0;
computer(head);
return maxSum;
}
private void computer(ListNode head) {
if (head == null) {
return;
}
computer(head.next);
maxSum = Math.max(maxSum, head.val + prev.val);
prev = prev.next;
}
Delete the Middle Node of a Linked Li
You are given the head of a linked list. Delete the middle node, and return the head of the modified linked list.
The middle node of a linked list of size n is the ⌊n / 2⌋th node from the start using 0-based indexing, where ⌊x⌋ denotes the largest integer less than or equal to x.
For n = 1, 2, 3, 4, and 5, the middle nodes are 0, 1, 1, 2, and 2, respectively.
Input: head = [1,3,4,7,1,2,6]
Output: [1,3,4,1,2,6]
Explanation:
The above figure represents the given linked list. The indices of the nodes are written below.
Since n = 7, node 3 with value 7 is the middle node, which is marked in red.
We return the new list after removing this node.
public ListNode deleteMiddle(ListNode head) {
if (head == null || head.next == null) {
return null;
}
ListNode node = head;
ListNode slow = head, fast = head;
while (fast != null && fast.next != null) {
fast = fast.next.next;
node = slow;
slow = slow.next;
}
node.next = slow.next;
return head;
}
dummy head
public ListNode deleteMiddle(ListNode head) {
ListNode dummy = new ListNode(-1), slow = dummy, fast = dummy;
dummy.next = head;
while (fast.next != null && fast.next.next != null) {
slow = slow.next;
fast = fast.next.next;
}
slow.next = slow.next.next;
return dummy.next;
}
Convert Sorted List to Binary Search Tree 109
Given the head of a singly linked list where elements are sorted in ascending order, convert it to a height balanced BST.
For this problem, a height-balanced binary tree is defined as a binary tree in which the depth of the two subtrees of every node never differ by more than 1.
Input: head = [-10,-3,0,5,9]
Output: [0,-3,9,-10,null,5]
Explanation: One possible answer is [0,-3,9,-10,null,5], which represents the shown height balanced BST.
time: O(nlong)
space: time: O(nlong)
每次找中点, 想象成一条绳,提起中点作为根节点,分出左右两部分,再提起各自的中点作为根节点……分治下去,这根绳就成了 BST 的模样
public TreeNode sortedListToBST(ListNode head) {
if(head == null)return null;
ListNode slow = head, fast = head, pre = null;
while(fast != null && fast.next != null){
pre = slow;
slow = slow.next;
fast = fast.next.next;
}
TreeNode root = new TreeNode(slow.val);
root.right = sortedListToBST(slow.next);
if (pre != null) {
pre.next = null;
root.left = sortedListToBST(head);
}
return root;
}
Convert linked list to array then do PreOrder Traversal
arr[mid] as the root
(left, mid - 1) as the left sub
(mid + 1, right) as the right sub
time: O(N)
space: time: O(N)
public TreeNode sortedListToBST(ListNode head) {
List<Integer> arr = new ArrayList<>();
while (head != null) {
arr.add(head.val);
head = head.next;
}
return helper(arr, 0, arr.size() - 1);
}
TreeNode helper(List<Integer> arr, int left, int right) {
if (left > right) {
return null;
}
int mid = left + (right - left) / 2;
TreeNode root = new TreeNode(list.get(mid));
root.left = helper(list, left, mid - 1);
root.right = helper(list, mid + 1, right);
return root;
}
中序遍历
时间复杂度:O(n)
空间复杂度:O(logn)
方法 1 每次获取数组中点:O(1),方法 2 每次获取链表中点:O(N),所以更慢。
其实直接获取链表头结点:O(1)O(1),不如直接构建它吧!它对应 BST 最左子树的根节点。
于是我们先构建左子树,再构建根节点,再构建右子树。——遵循中序遍历。
其实,BST 的中序遍历,打印的节点值正是这个有序链表的节点值顺序。
如下图,维护指针 h,从头结点开始,用 h.val 构建节点,构建一个,指针后移一位。
求出链表结点总个数,用于每次二分求出链表的中点。
为什么要这么做,因为我们构建的节点值是:从小到大,我们希望在递归中处理节点的顺序和链表结点顺序一一对应
看看下图的递归树,感受一下二分法怎么做到的。
用二分后的左链,递归构建左子树,然后用 h.val 创建节点,接上创建好的左子树,再用右链构建右子树,再接上。
递归中会不断进行二分,直到无法划分就返回 null,即来到递归树的底部
h.val 创建完结点后,h 指针就后移,锁定出下一个要构建的节点值
ListNode head;
public TreeNode sortedListToBST(ListNode head) {
this.head = head;
return helper(0, length(head) - 1);
}
TreeNode helper(int left, int right) {
if (left > right) {
return null;
}
int mid = left + (right - left) / 2;
TreeNode leftNode = helper(left, mid - 1); // 先递归构建左子树
TreeNode root = new TreeNode(head.val); // // 根据 h.val 构建节点
head = head.next; // // h指针步进
root.left = leftNode;
root.right = helper(mid + 1, right);
return root;
}
int length(ListNode head) {
int res = 0;
while (head != null) {
head = head.next;
res++;
}
return res;
}
Car Fleet II 1776
There are n cars traveling at different speeds in the same direction along a one-lane road. You are given an array cars of length n, where cars[i] = [positioni, speedi] represents:
positioni is the distance between the ith car and the beginning of the road in meters. It is guaranteed that positioni < positioni+1.
speedi is the initial speed of the ith car in meters per second.
For simplicity, cars can be considered as points moving along the number line. Two cars collide when they occupy the same position. Once a car collides with another car, they unite and form a single car fleet. The cars in the formed fleet will have the same position and the same speed, which is the initial speed of the slowest car in the fleet.
Return an array answer, where answer[i] is the time, in seconds, at which the ith car collides with the next car, or -1 if the car does not collide with the next car. Answers within 10-5 of the actual answers are accepted.
Example 1:
Input: cars = [[1,2],[2,1],[4,3],[7,2]]
Output: [1.00000,-1.00000,3.00000,-1.00000]
Explanation: After exactly one second, the first car will collide with the second car, and form a car fleet with speed 1 m/s. After exactly 3 seconds, the third car will collide with the fourth car, and form a car fleet with speed 2 m/s.
Imagine a,b,c on the road, if the a catches b later than b catched c, then a won’t catch b but b+c
Complexity
Time O(n)
Space O(n)
a, b, c, d, 如果 c 追上了 d, b 就有 3 个情况: 能追上; 追不上 c, 但是追上 d; c, d 都追不上
此处的详细说明:
- 如果当前车的车速 <= 栈顶车的车速,则当前车永远无法追上栈顶车,因此总是可以 pop 出栈顶车;
- 否则,如果当前车的车速 > 栈顶车: 2.1 如果栈顶车的追上更右侧车辆的时间为 -1 (永远追不上),则不能 pop 出; 2.2 否则,则判断在 “理想状态(即栈顶车不会追上更右侧车)”下 ,当前车的追上栈顶车的时间 T (也就是下面代码里的式子),如果 T > resst.top(), 说明不能在右侧车追上更右侧车之前追上,应当 pop;否则能在碰撞前追上。
public double[] getCollisionTimes(int[][] cars) {
int n = cars.length;
Deque<Integer> stack = new ArrayDeque<>();
double[] res = new double[n];
for (int i = n - 1; i >= 0; i--) {
res[i] = -1.0;
int p = cars[i][0], s = cars[i][1];
while (stack.size() > 0) {
int j = stack.peekLast(), p2 = cars[j][0], s2 = cars[j][1];
/** Now we have either one of situations
1. c1 is slower than c2
2. c1 potentially catches c2 AFTER c2 vanishes
Claim: no car before c1 will vanish into c2
1. ==> cars before c1 will vanish into c1 first before catching c2
2. <==> c2 "vanishes" into another car even before c1 catches it
Either way, c2 can not be catched by c1 or cars beofre c1 ==> poll it out from stack
*/
if (s <= s2 || 1.0 * (p2 - p) / (s - s2) >= res[j] && res[j] > 0) {
stack.pollLast();
} else {
break;
}
}
if (stack.size() > 0) {
int j = stack.peekLast(), p2 = cars[j][0], s2 = cars[j][1];
res[i] = 1.0 * (p2 - p) / (s - s2);
}
stack.add(i);
}
return res;
}
O(N\log N)O(NlogN)
一个相对直观的思路是:我们按照时间大小顺序,先找出最先相遇的两辆车,再找出随后相遇的两辆车,最终找出最后相遇的两辆车。由于两辆车相遇后会「变为一辆车」,因此最多找 n-1n−1 次即可。
我们使用优先队列来维护这一关系。优先队列的每个元素 \textit{Node}Node 代表每次「相遇」,它具有三个属性:距离起点较近的车 \textit{low}low,距离起点较远的车 \textit{high}high,以及它们相撞所需的时间 tt。
初始时,最先相撞的两辆车,一定来自两辆直接相邻的车。因此,我们首先遍历 \textit{cars}cars 数组,将 n-1n−1 对相邻的车加入到优先队列当中。
随后,我们不断取出优先队列的头部元素 \textit{Node}Node,随后:
将第 \textit{Node}.\textit{low}Node.low 辆车的相遇时间设置为 \textit{Node}.\textit{t}Node.t,放入结果数组中。 将第 \textit{Node}.\textit{low}Node.low 辆车以某种形式「删除」。因为两车相遇后,由于两车的速度都变为较慢车的速度,故随后的时间里就只需要考虑第 \textit{Node}.\textit{high}Node.high 辆车。 第 \textit{Node}.\textit{low}Node.low 辆车被删除后,离第 \textit{Node}.\textit{high}Node.high 辆车后面最近的那辆车也发生了变化。因此,要找出删除后离第 \textit{Node}.\textit{high}Node.high 辆车后面最近的那辆车,并将该车与第 \textit{Node}.\textit{high}Node.high 辆车放入优先队列当中
class Node {
int id; // car_id
double time; // the time for collision with the next car
public Node(int _id, double _time) {
id = _id;
time = _time;
}
}
public double[] getCollisionTimes(int[][] cars) {
PriorityQueue<Node> pq = new PriorityQueue<>(200000, (a, b) -> Double.compare(a.time, b.time));
int n = cars.length;
for (int i = 0; i < n - 1; ++i) {
if (cars[i][1] > cars[i+1][1]) { // if there could be collision for i-th car and i+1-th car
pq.offer(new Node(i, (double)(cars[i+1][0] - cars[i][0]) / (double)(cars[i][1] - cars[i+1][1])));
}
}
double[] res = new double[n];
Arrays.fill(res, -1.0);
TreeSet<Integer> ts = new TreeSet<>(); // used to record all alive cars
for (int i = 0; i < n; ++i) {
ts.add(i);
}
while (!pq.isEmpty()) {
Node cur = pq.poll();
if (res[cur.id] != -1.0) // this means such car is already processed in previous steps
continue;
res[cur.id] = cur.time;
if (ts.lower(cur.id) == null) // if there is no previous car, no need for update
continue;
int prev = ts.lower(cur.id); // find the previous alive car
int next = ts.higher(cur.id); // find the next car, since this is the next car of the previous car now
if (cars[prev][1] > cars[next][1]) { // update the information of previous car
pq.offer(new Node(prev, (double)(cars[next][0] - cars[prev][0]) / (double)(cars[prev][1] - cars[next][1])));
}
ts.remove(cur.id); // such car is dead, remove it
}
return res;
}
😼😼😼😼
来源:力扣(LeetCode) 链接:https://leetcode-cn.com/problems/MPnaiL
感谢:她们都有题库在 github 上直接有,都是大神, 都富有详细解法,对新人特别适合了解解题思路
