about Dynamic Programming
about Dynamic Programming learing note
- steps to solve a dynamic programming problems
- sp1. dp table and index meaning
- sp2. recurrence formula
- sp3. initial values
- sp4. literacy directions
- sp5. cases
- Q.1: Climbing Stairs
- Q.2: Min Cost Climbing Stairs
- Q.3: Unique Paths
- Q.4:Unique Paths II
- Q.5:Integer Break
- Q.6:BackPack
- Q.7:Partition Equal Subset Sum
- Q.8:Last Stone Weight II
- Q.9:Target Sum
- Q.10:Last Stone Weight II
- Q.11:Coin Change 2
- Q.12:Combination Sum IV
- Q.13:Climbing Stairs improve
- Q.14:Coin Change
- Q.15:Perfect Squares
- Q.16:Word Break
- Q.17:House Robber
- Q.18:House Robber II
- Q.20: Best Time to Buy and Sell Stock
- Q.19: House Robber III
- Q.20: Best Time to Buy and Sell Stock
- Q.21: Best Time to Buy and Sell Stock II
- Q.22: Best Time to Buy and Sell Stock III
- Q.23: Best Time to Buy and Sell Stock III
- Q.24: Best Time to Buy and Sell Stock with Cooldown
- Q.25: Maximum Length of Repeated Subarray
- Q.26: Longest Common Subsequence
- Q.27: Uncrossed Lines
- Q.28: Is Subsequence
- Q.29: Distinct Subsequences
- Q.30: Delete Operation for Two Strings
- Q.31: Edit Distance
- Q.32: Palindromic Substrings
- Q.33: Palindromic Subsequence
- Q.34: Triangle
- Q.35: Minimum Falling Path Sum
- Q.36: Count All Possible Routes
- Q.37: Minimum Falling Path Sum II
steps to solve a dynamic programming problems
sp1. dp table and index meaning
sp2. recurrence formula
sp3. initial values
sp4. literacy directions
sp5. cases
Q.1: Climbing Stairs
https://leetcode-cn.com/problems/climbing-stairs/
You are climbing a staircase. It takes n steps to reach the top.
Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?
- sp1. dp table and index meaning
dp[i]: reach to the ith stairs, have dp[i] methods
- sp2. recurrence formula
dp[i - 1], reach to the i - 1 th stairs, take one step = dp[i]
dp[i - 2], reach to the i - 2 th stairs, take two steps at onece = dp[i]
dp[i] = dp[i - 1] + dp[i -2]
- sp3. initial values
dp[1] = 1, dp[2] = 2, //here dp[0] has no meaning
- sp4. literacy directions
front to back
- sp5. cases
n = 5
i : 1 2 3 4 5
dp[i]: 1 2 3 5 8
Q.2: Min Cost Climbing Stairs
https://leetcode-cn.com/problems/min-cost-climbing-stairs/
You are given an integer array cost where cost[i] is the cost of ith step on a staircase. Once you pay the cost, you can either climb one or two steps.
You can either start from the step with index 0, or the step with index 1.
Return the minimum cost to reach the top of the floor.
- sp1. dp table and index meaning
dp[i]: reach to the ith stairs, have the least costs dp[i]
- sp2. recurrence formula
dp[i - 1] or dp[i - 2] 2 choices
dp[i] = min(dp[i - 1], dp[i -2]) + cost[i];
- sp3. initial values
dp[0] = cost[0], dp[1] = cost[1]
- sp4. literacy directions
front to back
- sp5. cases
cpst = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1]
i : 0 1 2 3 4 5 6 7 8 9
dp[i]: 1 100 2 3 3 103 4 5 104 6
Q.3: Unique Paths
https://leetcode-cn.com/problems/unique-paths/
A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).
The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked 'Finish' in the diagram below).
How many possible unique paths are there?
- sp1. dp table and index meaning
dp[m][n]: reach to the (i, j) stairs, have dp[m][n] choices
- sp2. recurrence formula
dp[m][n] = dp[m - 1][n] + dp[m][n -1]
- sp3. initial values
dp[i][0] = 1; from(0, 0) to (i, 0) has only one path; for (int i = 0; i < m; i++)>)
dp[0][j] = 1; from(0, 0) to (0, j) has only one path;
- sp4. literacy directions
left to right
- sp5. cases
m = 3, n = 7,
: 1 1 1 1 1 1 1
: 1 2 3 4 5 6 7
: 1 3 6 10 15 21 28
O(M*N), O(N)
reducing space complexity
dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
dp[j] = dp[j] + dp[j - 1]
O(M*N), O(N)
class Solution {
public int uniquePaths(int m, int n) {
//一维空间,其大小为 n
int[] dp = new int[n];
Arrays.fill(dp, 1);
for(int i = 1; i < m; ++i) {
for(int j = 1; j < n; ++j) {
//等式右边的 dp[j]是上一次计算后的,加上左边的dp[j-1]即为当前结果
dp[j] = dp[j] + dp[j - 1];
}
}
return dp[n - 1];
}
}
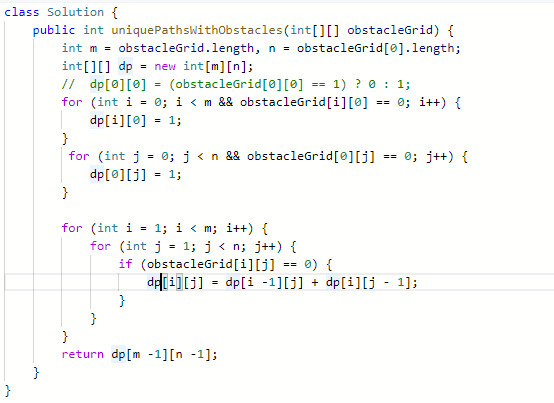
Q.4:Unique Paths II
A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).
The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked 'Finish' in the diagram below).
Now consider if some obstacles are added to the grids. How many unique paths would there be?
An obstacle and space is marked as 1 and 0 respectively in the grid.
- sp1. dp table and index meaning
dp[m][n]: reach to the (i, j) stairs, have dp[m][n] choices
- sp2. recurrence formula
if (obstacleGrid[i][j] == 0) { dp[i][j] = dp[i - 1][j] + dp[i][j -1] }
- sp3. initial values
dp[i][0] = 1; from(0, 0) to (i, 0) has only one path; for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++)>)
dp[0][j] = 1; from(0, 0) to (0, j) has only one path; for (int i = 0; i < n && obstacleGrid[0][i] == 0; i++)
- sp4. literacy directions
left to right
- sp5. cases
m = 3, n = 7,
: 1 1 1
: 1 0 1
: 1 1 2
Unique Paths II
Q.5:Integer Break
https://leetcode-cn.com/problems/integer-break/
Given an integer n, break it into the sum of k positive integers, where k >= 2, and maximize the product of those integers.
Return the maximum product you can get.
- sp1. dp table and index meaning
dp[i]: number i, get maximize result dp[i]
- sp2. recurrence formula
j * (i -j)
j * dp[i - j]
dp[i] = max(dp[i], max((i - j) * j, dp[i - j]* j));
- sp3. initial values
dp[2] = 1
- sp4. literacy directions
front to back
- sp5. cases
n = 10
i : 2 3 4 5 6 7 8 9 10
dp[i] : 1 2 4 6
large left, small right
dp[2] = 1
dp[3]: 2
case 1: max(2, dp[2]) * 1
dp[4]: 4
case 1: max(3, dp[3]) * 1
case 2: max(2, dp[2]) * 2
dp[5]: 6
case 1: max(4, dp[4]) * 1
case 2: max(3, dp[3]) * 2
case 3: max(2, dp[2]) * 3
dp[6]: 9
case 1: max(5, dp[5]) * 1
case 1: max(4, dp[4]) * 2
case 2: max(3, dp[3]) * 3
case 3: max(2, dp[2]) * 4
Q.6:BackPack
return the max value of the backpack
maxweight = 4
items: weight value
item0: 1 15
item1: 3 20
item2: 4 30
- sp1. dp table and index meaning
dp[i][j]: [0-i]items, put in j weight backpack, return a max value
- sp2. recurrence formula
no more item: dp[i][j] = dp[i -1][j]
add item i: dp[i][j] = dp[i -1][j - weight[i]] + value[i]
dp[i] = max(dp[i -1][j], dp[i - 1][j - weight[i] + value[i]]);
- sp3. initial values backpack weight: j dp[i][j]
if j = 0, and j < weight[0], dp[i][0] = 0, because no items can put in the backpack if i = 0, jfor (int j = weight[0]; j <= bagWeight; j++) ; dp[0][j] = value[0];
0 1 2 3 4
item0: 0 15 15 15 15
item1: 0
item2: 0
- sp4. literacy directions
front to back
- sp5. cases
maxweight = 4
items: weight value
item0: 1 15
item1: 3 20
item2: 4 30
0 1 2 3 4
item0: 0 15 15 15 15
item1: 0 15 15 20 35
item2: 0 15 15 20 35
return dp[2][4]
public static void main(String[] args) {
int[] weight = {1, 3, 4};
int[] value = {15, 20, 30};
int bagSize = 4;
testWeightBagProblem(weight, value, bagSize);
}
public static void testWeightBagProblem(int[] weight, int[] value, int bagSize){
int wLen = weight.length, value0 = 0;
//定义dp数组:dp[i][j]表示背包容量为j时,前i个物品能获得的最大价值
int[][] dp = new int[wLen + 1][bagSize + 1];
//初始化:背包容量为0时,能获得的价值都为0
for (int i = 0; i <= wLen; i++){
dp[i][0] = value0;
}
//遍历顺序:先遍历物品,再遍历背包容量
for (int i = 1; i <= wLen; i++){
for (int j = 1; j <= bagSize; j++){
if (j < weight[i - 1]){
dp[i][j] = dp[i - 1][j];
}else{
dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weight[i - 1]] + value[i - 1]);
}
}
}
//打印dp数组
for (int i = 0; i <= wLen; i++){
for (int j = 0; j <= bagSize; j++){
System.out.print(dp[i][j] + " ");
}
System.out.print("\n");
}
}
reducing space complexity
dp[j]为 容量为 j 的背包所背的最大价值,那么如何推导 dp[j]呢?
dp[j]可以通过 dp[j - weight[i]]推导出来,dp[j - weight[i]]表示容量为 j - weight[i]的背包所背的最大价值。
dp[j - weight[i]] + value[i] 表示 容量为 j - 物品 i 重量 的背包 加上 物品 i 的价值。(也就是容量为 j 的背包,放入物品 i 了之后的价值即:dp[j])
此时 dp[j]有两个选择,一个是取自己 dp[j] 相当于 二维 dp 数组中的 dp[i-1][j],即不放物品 i,一个是取 dp[j - weight[i]] + value[i],即放物品 i,指定是取最大的,毕竟是求最大价值,
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
dp[i] = max(dp[i -1][j], dp[i - 1][j - weight[i] + value[i]]);
public static void main(String[] args) {
int[] weight = {1, 3, 4};
int[] value = {15, 20, 30};
int bagSize = 4;
testWeightBagProblem(weight, value, bagSize);
}
public static void testWeightBagProblem(int[] weight, int[] value, int bagSize){
int wLen = weight.length, value0 = 0;
//定义dp数组:dp[j]表示背包容量为j时,获得的最大价值
int[] dp = new int[bagSize + 1];
//遍历顺序:先遍历物品,再遍历背包容量
for (int i = 0; i <= wLen; i++){
// need reverse iterate
for (int j = bagSize; j >= weight[i]; j--){
dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);
}
}
}
//打印dp数组
for (int j = 0; j <= bagWeight; j++){
System.out.print(dp[j] + " ");
}
}
maxweight = 4
items: weight value
item0: 1 15
item1: 3 20
item2: 4 30
0 1 2 3 4
item0: 0 15 15 15 15
item1: 0 15 15 20 35
item2: 0 15 15 20 35
0 1 2 3 4
item0: 0 15 15 15 15
Q.7:Partition Equal Subset Sum
https://leetcode-cn.com/problems/partition-equal-subset-sum/
Given a non-empty array nums containing only positive integers, find if the array can be partitioned into two subsets such that the sum of elements in both subsets is equal.
This is a Knapsack problem,
- sp1. dp table and index meaning
dp[i][j]: whether we can sum to j using first i numbers
- sp2. recurrence formula
dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);
- sp3. initial values
dp[0] = 0
- sp4. literacy directions
for (int i = 0; i < nums.length(); i++) { for (int j = target; j >= nums[i]; j–) { dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]); } }
- sp5. cases
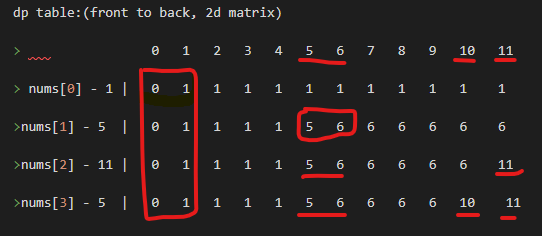
[1, 5, 11, 5], target = 11
nums[0] 1: 0 1 2 3 4 5 6 7 8 9 10 11
Pint: <-- 0 1 1 1
nums[1] 5 : 0 1 2 3 4 5 6 7 8 9 10 11
Pint: <-- 0 1 5 6 6 6
nums[2] 11: 0 1 2 3 4 5 6 7 8 9 10 11
Pint: <-- 0 1 5 6 6 11
nums[3] 5: 0 1 2 3 4 5 6 7 8 9 10 11
Pint: <-- 0 1 5 6 10 11
nums[0] - 1 {0, 1}
nums[1] - 5 {0, 1, 5, 6}
nums[2] - 11 {0, 1, 5, 6, 11}
nums[3] - 5 {0, 1, 5, 6, 11, 10}
dp table:(front to back, 2d matrix)
Partition Equal Subset Sum
// i = 0, the first item
if (nums[0] <= target) {
dp[0][nums[0]] = 0;
}
for (int i = 1; i < len; i++) {
for (int j = 0; j <= target; j++) {
}
}
dp :(back to front, one dimension dp)
once nums[i] <= j, get to the next loop

Partition Equal Subset Sum
time:O(n^2) space:O(n)
Q.8:Last Stone Weight II
https://leetcode-cn.com/problems/last-stone-weight-ii/
You are given an array of integers stones where stones[i] is the weight of the ith stone.
We are playing a game with the stones. On each turn, we choose any two stones and smash them together. Suppose the stones have weights x and y with x <= y. The result of this smash is:
If x == y, both stones are destroyed, and
If x != y, the stone of weight x is destroyed, and the stone of weight y has new weight y - x.
At the end of the game, there is at most one stone left.
Return the smallest possible weight of the left stone. If there are no stones left, return 0.
- sp1. dp table and index meaning
dp[j]: bag j, get maximize weight dp[j]
- sp2. recurrence formula
dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);
- sp3. initial values
dp[0] = 0
- sp4. literacy directions
for (int i = 0; i < stones.length(); i++) { for (int j = target; j >= stones[i]; j–) { dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]); } }
- sp5. cases
[2, 4, 1, 1], target = 4
j : 0 1 2 3 4
2 : 0 0 2 2 2
4 : 0 0 2 2 4
1 : 0 1 2 3 4
1 : 0 1 2 3 4
result = sum - 2 * dp[target]
Q.9:Target Sum
https://leetcode-cn.com/problems/target-sum/
You are given an integer array nums and an integer target.
You want to build an expression out of nums by adding one of the symbols '+' and '-' before each integer in nums and then concatenate all the integers.
For example, if nums = [2, 1], you can add a '+' before 2 and a '-' before 1 and concatenate them to build the expression "+2-1".
Return the number of different expressions that you can build, which evaluates to target.
target = positive sum(left) - negative sum(right);
left - right = target
left + right = sum;
left = (sum + target) / 2
- sp1. dp table and index meaning
dp[j]: sum j, get maximize method dp[j]
- sp2. recurrence formula
dp[j] += dp[j - nums[i]];
- sp3. initial values
dp[0] = 1,
- sp4. literacy directions use one dimension dp
- sp5. cases
[1, 1, 1, 1, 1], target = 3, bagsize = (3 + 4) /2 = 4;
b : 0 1 2 3 4 dp[j] += dp[j - nums[i]]; dp[4] += dp[3], dp[3] += dp[2]; dp[2] += dp[1]; dp[1] += dp[0];
1 : 1 1 0 0 0
1 : 1 2 1 0 0
1 : 1 3 3 1 0
1 : 1 4 6 4 1
1 : 1 5 10 10 5
details explains:
int sum = 0;
for (int i = 0; i < nums.length; i++) sum += nums[i];
if ((target + sum) % 2 != 0) return 0;
int size = (target + sum) / 2;
if(size < 0) size = -size;
int[] dp = new int[size + 1];
dp[0] = 1;
for (int i = 0; i < nums.length; i++) {
for (int j = size; j >= nums[i]; j--) {
dp[j] += dp[j - nums[i]];
}
}
return dp[size];
}
sum = pos_sum + neg_sum;
(sum - target) % 2 == 0, because the num in nums are all pos_Integer;
inition:
b : 0 1 2 3 4
1 : 1 0 0 0 0
1 : 1 0 0 0 0
1 : 1 0 0 0 0
1 : 1 0 0 0 0
1 : 1 0 0 0 0
after the first row:
b : 0 1 2 3 4
1 : 1 1 0 0 0 <—-
1 : 1 1 0 0 0
1 : 1 1 0 0 0
1 : 1 1 0 0 0
1 : 1 1 0 0 0
after the second row:
b : 0 1 2 3 4
1 : 1 1 0 0 0
1 : 1 2 1 0 0 <—-
1 : 1 2 1 0 0 dp[j]
1 : 1 2 1 0 0
1 : 1 2 1 0 0
after the third row:
b : 0 1 2 3 4
1 : 1 1 0 0 0
1 : 1 2 1 0 0
1 : 1 3 3 1 0 <—- dp[j]
1 : 1 3 3 1 0
1 : 1 3 3 1 0
Q.10:Last Stone Weight II
https://leetcode-cn.com/problems/ones-and-zeroes/
You are given an array of binary strings strs and two integers m and n.
Return the size of the largest subset of strs such that there are at most m 0's and n 1's in the subset.
A set x is a subset of a set y if all elements of x are also elements of y.
- sp1. dp table and index meaning
dp[i][j]: the max size of dp[i][j], has i’s 0, j’s 1;
- sp2. recurrence formula
dp[i][j] = max(dp[i][j], dp[i - zeroNums][j - oneNums] + 1);
- sp3. initial values
dp[0][0] = 0
- sp4. literacy directions
for (int i = m; i >= zeroNum; i–) { for (int j = n; j >= oneNum; j–) { dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1); } }
- sp5. cases
[10, 0001, 111001, 1, 0], m = 3, n = 3
j : 0 1 2 3
0 : 0 0 0 0 <—- Z: 1; O: 1 dp[3][3] = dp[2][2]
1 : 0 0 0 0 <—- Z: 3; O: 1 dp[3][3] = dp[0][2]
2 : 0 0 0 0 <—- Z: 0; O: 1 dp[1][1] = dp[1][0]
3 : 0 1 1 1
details:
every string is a item,
dp[i][j][k] : in [0, i], it can max numbers of j’s 0, k’s 1;
dp[i][j][k] = dp[i - 1][j][k] ;
dp[i][j][k] = dp[i - 1][j - zeroNum][k - oneNum] + 1 ;
int len = strs.length;
int[][][] dp = new int[len + 1][m + 1][n + 1];
for (int i = 1; i <= len; i++) {
int[] count = countZeroAndOne(Strs[i - 1]);
for (int j = 0; j <= m; j++) {
for (int k = 0; k <= n; j++) {
dp[i][j][k] = dp[i - 1][j][k];
int zeros = count[0];
int ones = count[1];
if (j >= zeros && k >= ones) {
dp[i][j][k] = Math.max(dp[i - 1][j][k], dp[i - 1][j - zeros][k - ones]);
}
}
}
return dp[len][m][n];
}
private int[] countZeroAndOne(String str) {
int[] cnt = new int[2];
for (char c : str.toCharArray()) {
cnt[c - '0']++;
}
return cnt;
}
Q.11:Coin Change 2
https://leetcode-cn.com/problems/coin-change-2/
You are given an integer array coins representing coins of different denominations and an integer amount representing a total amount of money.
Return the number of combinations that make up that amount. If that amount of money cannot be made up by any combination of the coins, return 0.
You may assume that you have an infinite number of each kind of coin.
The answer is guaranteed to fit into a signed 32-bit integer.
- sp1. dp table and index meaning
dp[j]: the max ways to reach amount dp[j];
- sp2. recurrence formula
dp[j] =dp[j] + dp[j - nums[i]];
- sp3. initial values
dp[0] = 1
- sp4. literacy directions
for (int i = 0; i < coins.size(); i++) { for (int j = coins[i]; j <= amount; j++) { dp[j] += dp[j - coins[i]]; // dp[0] must be 1; } }
- sp5. cases
[1, 2, 5], amount = 5
j : 0 1 2 3 4 5
1 : 1 1 1 1 1 1
2 : 1 1 2 2 3 3
5 : 1 1 2 2 3 4
Q.12:Combination Sum IV
https://leetcode-cn.com/problems/combination-sum-iv/
Given an array of distinct integers nums and a target integer target, return the number of possible combinations that add up to target.
The answer is guaranteed to fit in a 32-bit integer.
- sp1. dp table and index meaning
dp[i]: the max ways to reach amount dp[i];
- sp2. recurrence formula
dp[i] =dp[i] + dp[i - nums[j]];
- sp3. initial values
dp[0] = 1
- sp4. literacy directions
Combination: outer loop is items, inner loop is Knapsack
Permutation: outer loop is Knapsack, inner loop is items
- sp5. cases
[1, 2, 3], amount = 4
i : 0 1 2 3 4
1 : 1 1 2 4 7
dp[1] = dp[0] = 1
dp[2] = dp[1] + dp[0] = 2;
dp[3] = dp[2] + dp[1] + dp[0] = 4;
dp[4] = dp[3] + dp[2] + dp[1] + dp[0] = 7;
for (int i = 0; i <= target; i++) {
for (int j = 0; j <= nums.length; j++) {
if (i > nums[j]) {
dp[i] += dp[i - nums[j]];
}
}
}
return dp[target];
Q.13:Climbing Stairs improve
You are climbing a staircase. It takes n steps to reach the top.
Each time you can either climb 1 or 2 , 3 ---- to m steps. In how many distinct ways can you climb to the top?
- sp1. dp table and index meaning
dp[i]: the max ways to reach the top dp[i];
- sp2. recurrence formula
dp[i] += dp[i - j];
- sp3. initial values
dp[0] = 1
- sp4. literacy directions
Combination: outer loop is items, inner loop is Knapsack
Permutation: outer loop is Knapsack, inner loop is items
- sp5. cases
int[] dp = new int[n + 1];
int[] weight = {1, 2};
dp[0] = 1;
for (int i = 0; i <= n; i++) {
for (int j = 0; j <= weight.length; j++) {
if (i > weight[j]) {
dp[i] += dp[i - weight[j]];
}
}
}
return dp[n];
Q.14:Coin Change
You are given an integer array coins representing coins of different denominations and an integer amount representing a total amount of money.
Return the fewest number of coins that you need to make up that amount. If that amount of money cannot be made up by any combination of the coins, return -1.
You may assume that you have an infinite number of each kind of coin.
- sp1. dp table and index meaning
dp[j]: the min coins need to reach the amount j ;
- sp2. recurrence formula
dp[j] = min(dp[j], dp[j - coins[i]]);
- sp3. initial values
dp[0] = 0;
the rest non-zero index should be Integer_MAX;
- sp4. literacy directions
Combination: outer loop is items, inner loop is Knapsack
Permutation: outer loop is Knapsack, inner loop is items
- sp5. cases
[1, 2, 5], amount = 5
i : 0 1 2 3 4 5
dp[j] : 0 1 1 2 2 1
Q.15:Perfect Squares
Given an integer n, return the least number of perfect square numbers that sum to n.
A perfect square is an integer that is the square of an integer; in other words, it is the product of some integer with itself. For example, 1, 4, 9, and 16 are perfect squares while 3 and 11 are not.
- sp1. dp table and index meaning
dp[i]:
- sp2. recurrence formula
dp[j] = dp[j - i * i];
- sp3. initial values
dp[0] = 0;
the rest non-zero index should be Integer_MAX;
- sp4. literacy directions
Combination: outer loop is items, inner loop is Knapsack
Permutation: outer loop is Knapsack, inner loop is items
- sp5. cases
n = 5
i : 0 1 2 3 4 5
dp[i] : 0 1 1 2 2 1
Q.16:Word Break
https://leetcode-cn.com/problems/word-break/
Given a string s and a dictionary of strings wordDict, return true if s can be segmented into a space-separated sequence of one or more dictionary words.
Note that the same word in the dictionary may be reused multiple times in the segmentation.
- sp1. dp table and index meaning
dp[i]: string length at i, dp[i] is true, has one or multiple words in dict.
- sp2. recurrence formula
[0, j , i],
dp[j] is true, && words in [j, i] also in dict, then dp[i] is true;
- sp3. initial values
dp[0] = true;
the rest non-zero index should be false;
- sp4. literacy directions
Combination: outer loop is items, inner loop is Knapsack
Permutation: outer loop is Knapsack, inner loop is items
- sp5. cases
s = “leetcode”, wordDict = [“leet”, “code”]
i : 0 1 2 3 4 5 6 7 8
dp[i] : 1 0 0 0 1
Q.17:House Robber
https://leetcode-cn.com/problems/house-robber/
You are a professional robber planning to rob houses along a street. Each house has a certain amount of money stashed, the only constraint stopping you from robbing each of them is that adjacent houses have security systems connected and it will automatically contact the police if two adjacent houses were broken into on the same night.
Given an integer array nums representing the amount of money of each house, return the maximum amount of money you can rob tonight without alerting the police.
- sp1. dp table and index meaning
dp[i]: [0, i] get the max amount money dp[i]
- sp2. recurrence formula
dp[i] = max(dp[i -2] + nums[i], dp[i -1]);
- sp3. initial values
dp[0] = nums[0];
dp[1] = max(nums[0], nums[1]);
- sp4. literacy directions
front to back
- sp5. cases
[2, 7, 9, 3, 1]
i : 0 1 2 3 4
dp[i] : 2 7 11 11 12
Q.18:House Robber II
https://leetcode-cn.com/problems/house-robber-ii/
You are a professional robber planning to rob houses along a street. Each house has a certain amount of money stashed. All houses at this place are arranged in a circle. That means the first house is the neighbor of the last one. Meanwhile, adjacent houses have a security system connected, and it will automatically contact the police if two adjacent houses were broken into on the same night.
Given an integer array nums representing the amount of money of each house, return the maximum amount of money you can rob tonight without alerting the police.
- sp1. dp table and index meaning
dp[i]: [0, i] get the max amount money dp[i]
- sp2. recurrence formula
dp[i] = max(dp[i -2] + nums[i], dp[i -1]);
- sp3. initial values
Math.max(helper(nums, 0, n - 1), helper(nums, 1, n));
- sp4. literacy directions
front to back
- sp5. cases
[2, 7, 9, 3, 1]
i : 0 1 2 3 4
dp[i] :
Q.20: Best Time to Buy and Sell Stock
https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock/
You are given an array prices where prices[i] is the price of a given stock on the ith day.
You want to maximize your profit by choosing a single day to buy one stock and choosing a different day in the future to sell that stock.
Return the maximum profit you can achieve from this transaction. If you cannot achieve any profit, return 0.
- sp1. dp table and index meaning
tree dp, return int[val1, val2] : val1: not include current value, val2: include current value;
- sp3. initial values
if (cur == null) return int[]{0, 0};
- sp4. literacy directions
include root: int val1 = cur.val + left[0] + right[0];
not include root: int val2 = max(left[0], left[1]) + max(right[0], right[1]); return {val2, val1};
- sp5. cases
3{6, 7}
/ \
2{3, 2} 3{1, 3}
\ \
3{0, 3} 1{}
Q.19: House Robber III
https://leetcode-cn.com/problems/house-robber-ii/
The thief has found himself a new place for his thievery again. There is only one entrance to this area, called root.
Besides the root, each house has one and only one parent house. After a tour, the smart thief realized that all houses in this place form a binary tree. It will automatically contact the police if two directly-linked houses were broken into on the same night.
Given the root of the binary tree, return the maximum amount of money the thief can rob without alerting the police.
- sp1. dp table and index meaning
tree dp, return int[val1, val2] : val1: not include current value, val2: include current value;
- sp3. initial values
if (cur == null) return int[]{0, 0};
- sp4. literacy directions
include root: int val1 = cur.val + left[0] + right[0];
not include root: int val2 = max(left[0], left[1]) + max(right[0], right[1]); return {val2, val1};
- sp5. cases
3{6, 7}
/ \
2{3, 2} 3{1, 3}
\ \
3{0, 3} 1{}
Q.20: Best Time to Buy and Sell Stock
https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock/
You are given an array prices where prices[i] is the price of a given stock on the ith day.
You want to maximize your profit by choosing a single day to buy one stock and choosing a different day in the future to sell that stock.
Return the maximum profit you can achieve from this transaction. If you cannot achieve any profit, return 0.
-
sp1. dp table and index meaning
-
sp2. recurrence formula dp[i][0]:
-
i days hold stock
- i -1 days hold stock, the amount money: dp[i - 1][0]
- i buy the stock, the amount money: -prices[i]
- dp[i][0] = max(dp[i -1][0], -prices[i]);
dp[i][1]:
-
i days not hold stock
- i -1 days not hold stock, the amount money: dp[i - 1][1]
- i sell the stock, the amount money: dp[i - 1][0] + prices[i]
- dp[i][1] = max(dp[i -1][1], dp[i -1][0] + prices[i]);
-
sp3. initial values
dp[0][0] -= prices[0];
dp[0][1] = 0;
- sp4. literacy directions
front to back
- sp5. cases
[7, 1, 5, 3, 6, 4]
dp[i][0] dp[i][1]
-7 0
-1 0
-1 4
-1 4
-1 5
-1 5
Q.21: Best Time to Buy and Sell Stock II
https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-ii/
You are given an integer array prices where prices[i] is the price of a given stock on the ith day.
On each day, you may decide to buy and/or sell the stock. You can only hold at most one share of the stock at any time. However, you can buy it then immediately sell it on the same day.
Find and return the maximum profit you can achieve.
- sp1. dp table and index meaning
dp[i][0]:
- i days hold stock
- i -1 days hold stock, the amount money: dp[i - 1][0]
- i buy the stock, the amount money: dp[i -1][1] - prices[i]
- dp[i][0] = max(dp[i -1][0], dp[i -1][1]-prices[i]);
dp[i][1]:
-
i days not hold stock
- i -1 days not hold stock, the amount money: dp[i - 1][1]
- i sell the stock, the amount money: dp[i - 1][0] + prices[i]
- dp[i][1] = max(dp[i -1][1], dp[i -1][0] + prices[i]);
-
sp3. initial values
dp[0][0] -= prices[0];
dp[0][1] = 0;
- sp4. literacy directions
front to back
- sp5. cases
[7, 1, 5, 3, 6, 4]
dp[i][0] dp[i][1]
Q.22: Best Time to Buy and Sell Stock III
https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-iii/
You are given an array prices where prices[i] is the price of a given stock on the ith day.
Find the maximum profit you can achieve. You may complete at most two transactions.
Note: You may not engage in multiple transactions simultaneously (i.e., you must sell the stock before you buy again).
-
sp1. dp table and index meaning
the 5 situation of a day:
-
- do nothing
-
- the first time buy in
-
- the first time sell out
-
- the second time buy in
-
- the second time sell out
dp[i][j] , j [0, 4] situation
-
-
sp2. recurrence formula
dp[i][1]:
-
i days buy in stock:dp[i][1] = dp[i - 1][0] - prices[i];
-
i days do nothing, following i -1 buy in situation : dp[i][1] = dp[i - 1][1]
-
dp[i][1] = max(dp[i -1][1], dp[i -1][0]-prices[i]);
dp[i][2]:
-
i days sell out stock:dp[i][2] = dp[i - 1][1] + prices[i];
-
i days do nothing: dp[i][2] = dp[i - 1][2]
-
dp[i][2] = max(dp[i -1][2], dp[i -1][1] + prices[i]);
-
dp[i][3] = max(dp[i -1][3], dp[i -1][2] - prices[i]);
-
dp[i][4] = max(dp[i -1][4], dp[i -1][3] + prices[i]);
-
sp3. initial values
dp[0][0] = 0;
dp[0][1] -= prices[0];
dp[0][2] = 0;
dp[0][3] -= prices[0];
dp[0][4] = 0;
- sp4. literacy directions
front to back
- sp5. cases
[1, 2, 3, 4, 5]
i j 0 1 2 3 4
0 0 -1 0 -1 0
1 0 -1 1 -1 1
2 0 -1 2 -1 2
3 0 -1 3 -1 3
4 0 -1 4 -1 4
Q.23: Best Time to Buy and Sell Stock III
https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-iv/
You are given an integer array prices where prices[i] is the price of a given stock on the ith day, and an integer k.
Find the maximum profit you can achieve. You may complete at most k transactions.
Note: You may not engage in multiple transactions simultaneously (i.e., you must sell the stock before you buy again).
-
sp1. dp table and index meaning
the 5 situation of a day:
-
- do nothing
-
- the first time buy in
-
- the first time sell out
-
- the second time buy in
-
- the second time sell out
dp[i][j] , j [0, 2 * k + 1] situation
-
-
sp2. recurrence formula
dp[i][1]:
-
i days buy in stock:dp[i][1] = dp[i - 1][0] - prices[i];
-
i days do nothing, following i -1 buy in situation : dp[i][1] = dp[i - 1][1]
-
dp[i][1] = max(dp[i -1][1], dp[i -1][0]-prices[i]);
dp[i][2]:
-
i days sell out stock:dp[i][2] = dp[i - 1][1] + prices[i];
-
i days do nothing: dp[i][2] = dp[i - 1][2]
-
dp[i][2] = max(dp[i -1][2], dp[i -1][1] + prices[i]);
-
dp[i][3] = max(dp[i -1][3], dp[i -1][2] - prices[i]);
-
dp[i][4] = max(dp[i -1][4], dp[i -1][3] + prices[i]);
for (int j = 0; j < 2 * k -1; j += 2) {
dp[i][j + 1] = max(dp[i - 1][j + 1], dp[i - 1][j] - prices[i]);
dp[i][j + 2] = max(dp[i - 1][j + 2], dp[i - 1][j + 1] + prices[i]);
}
- sp3. initial values
dp[0][0] = 0;
dp[0][1] -= prices[0];
dp[0][2] = 0;
dp[0][3] -= prices[0];
dp[0][4] = 0;
for (int j = 1; j < 2 * k -1; j += 2) {
dp[0][j] = - prices[0];
}
- sp4. literacy directions
front to back
- sp5. cases
[1, 2, 3, 4, 5]
i j 0 1 2 3 4
0 0 -1 0 -1 0
1 0 -1 1 -1 1
2 0 -1 2 -1 2
3 0 -1 3 -1 3
4 0 -1 4 -1 4
Q.24: Best Time to Buy and Sell Stock with Cooldown
https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-with-cooldown/
You are given an array prices where prices[i] is the price of a given stock on the ith day.
Find the maximum profit you can achieve. You may complete as many transactions as you like (i.e., buy one and sell one share of the stock multiple times) with the following restrictions:
After you sell your stock, you cannot buy stock on the next day (i.e., cooldown one day).
Note: You may not engage in multiple transactions simultaneously (i.e., you must sell the stock before you buy again).
-
sp1. dp table and index meaning
the j situation of a day:
-
- buy in (or bought in before today)
-
- sell out and you can buy in anytime
-
- sell out today
-
- cooldown
-
-
sp2. recurrence formula
dp[i][0]:
- i-1 days bought in stock:dp[i][0] = dp[i - 1][0];
- i day buy in: i -1 is cooldown situdation: dp[i][3] - prices[i];
- i day buy in: i -1 is selling out situdation: dp[i][1] - prices[i];
dp[i][0] = max( dp[i - 1][0], max(dp[i][3] - prices[i], dp[i][1] - prices[i]));
dp[i][1]:
- i -1 days sell out stock:dp[i][1] = dp[i - 1][1] ;
- i -1 day is cooldown day: dp[i][2] = dp[i - 1][3]
dp[i][1] = max( dp[i - 1][1], dp[i -1][3]);
dp[i][2]:
- i -1 days buy in stock, and sell out today:dp[i][2] = dp[i - 1][0] + prices[i];
dp[i][2] = dp[i - 1][0] + prices[i];
dp[i][3]:
- i -1 days sell out stock:dp[i][3] = dp[i - 1][2];
dp[i][3] = dp[i - 1][2];
dp[i][0] = max( dp[i - 1][0], max(dp[i][3] - prices[i], dp[i][1] - prices[i]));
dp[i][1] = max( dp[i - 1][1], dp[i -1][3]);
dp[i][2] = dp[i - 1][0] + prices[i];
dp[i][3] = dp[i - 1][2];
- sp3. initial values
dp[0][0] = -= prices[0];
dp[0][1] = 0;
dp[0][2] = 0;
dp[0][3] = 0;
- sp4. literacy directions
front to back
- sp5. cases
[1, 2, 3, 0, 2]
i j 0 1 2 3
0 -1 0 0 0
1 -1 0 1 0
2 -1 0 2 1
3 1 1 -1 2
4 1 2 3 -1
Q.25: Maximum Length of Repeated Subarray
https://leetcode-cn.com/problems/maximum-length-of-repeated-subarray/
Given two integer arrays nums1 and nums2, return the maximum length of a subarray that appears in both arrays.
- sp1. dp table and index meaning
dp[i][j]: [0, i -1] and[0, j -1], the maximum length of repeated subarray
- sp2. recurrence formula
if (A[i -1] == B[j - 1]) dp[i][j]: dp[i - 1][j - 1] + 1
- sp3. initial values
dp[i][0] = 0;
dp[0][j] = 0;
- sp4. literacy directions
front to back
for (int i = 1; i <= A.length(); i++) {
for (int j = 1; j <= B.length(); j++) {
if (A[i -1] == B[j - 1]) {
dp[i][j] = dp[i - 1][j - 1] + 1;
}
if (dp[i][j] > res) res = dp[i][j];
}
- sp5. cases
A: [1, 2, 3, 2, 1] B: [3, 2, 1, 4, 7]
B: 3 2 1 4 7
0 0 0 0 0 0
1 0 0 0 1 0 0
2 0 0 1 0 0 0
3 0 1 0 0 0 0
2 0 0 2 0 0 0
1 0 0 0 3 0 0
Q.26: Longest Common Subsequence
https://leetcode-cn.com/problems/longest-common-subsequence/
Given two strings text1 and text2, return the length of their longest common subsequence. If there is no common subsequence, return 0.
A subsequence of a string is a new string generated from the original string with some characters (can be none) deleted without changing the relative order of the remaining characters.
For example, "ace" is a subsequence of "abcde".
A common subsequence of two strings is a subsequence that is common to both strings.
- sp1. dp table and index meaning
dp[i][j]: [0, i -1] and[0, j -1], the longest common of repeated Subsequence
- sp2. recurrence formula
if (A[i -1] == B[j - 1]) dp[i][j]: dp[i - 1][j - 1] + 1
if (A[i -1] != B[j - 1]) dp[i][j]: Math.max(dp[i - 1][j], dp[i][j - 1])
- sp3. initial values
dp[i][0] = 0;
dp[0][j] = 0;
- sp4. literacy directions
3 directions
| dp[i - 1][j - 1] | dp[i - 1][j] |
|---|---|
| dp[i][j - 1] dp[i][j] |
- sp5. cases
A: "abcde" B: "ace"
B: a c e
0 0 0 0
a 0 1 1 1
b 0 1 1 1
c 0 1 2 2
d 0 1 2 2
e 0 1 2 3
Q.27: Uncrossed Lines
https://leetcode-cn.com/problems/uncrossed-lines/
You are given two integer arrays nums1 and nums2. We write the integers of nums1 and nums2 (in the order they are given) on two separate horizontal lines.
We may draw connecting lines: a straight line connecting two numbers nums1[i] and nums2[j] such that:
nums1[i] == nums2[j], and
the line we draw does not intersect any other connecting (non-horizontal) line.
Note that a connecting line cannot intersect even at the endpoints (i.e., each number can only belong to one connecting line).
Return the maximum number of connecting lines we can draw in this way.
- sp1. dp table and index meaning
dp[i][j]: [0, i -1] and[0, j -1], the longest common of repeated Subsequence
- sp2. recurrence formula
if (A[i -1] == B[j - 1]) dp[i][j]: dp[i - 1][j - 1] + 1
if (A[i -1] != B[j - 1]) dp[i][j]: Math.max(dp[i - 1][j], dp[i][j - 1])
- sp3. initial values
dp[i][0] = 0;
dp[0][j] = 0;
- sp4. literacy directions
3 directions
| dp[i - 1][j - 1] | dp[i - 1][j] |
|---|---|
| dp[i][j - 1] dp[i][j] |
- sp5. cases
A: "abcde" B: "ace"
B: a c e
0 0 0 0
a 0 1 1 1
b 0 1 1 1
c 0 1 2 2
d 0 1 2 2
e 0 1 2 3
Q.28: Is Subsequence
https://leetcode-cn.com/problems/is-subsequence/
Given two strings s and t, return true if s is a subsequence of t, or false otherwise.
A subsequence of a string is a new string that is formed from the original string by deleting some (can be none) of the characters without disturbing the relative positions of the remaining characters. (i.e., "ace" is a subsequence of "abcde" while "aec" is not).
- sp1. dp table and index meaning
dp[i][j]: [0, i -1] and[0, j -1], the longest common of repeated Subsequence
- sp2. recurrence formula
if (A[i -1] == B[j - 1]) dp[i][j]: dp[i - 1][j - 1] + 1
if (A[i -1] != B[j - 1]) dp[i][j]: dp[i][j - 1]
- sp3. initial values
dp[i][0] = 0;
dp[0][0] = 0;
- sp4. literacy directions
3 directions
| dp[i - 1][j - 1] | dp[i - 1][j] |
|---|---|
| dp[i][j - 1] dp[i][j] |
- sp5. cases
A: "ahbgdc" B: "abc"
B: a h b g d c
0 0 0 0 0 0 0
a 0 1 1 1 1 1 1
b 0 0 0 2 2 2 2
c 0 0 0 0 0 0 3
Q.29: Distinct Subsequences
https://leetcode-cn.com/problems/distinct-subsequences/
Given two strings s and t, return the number of distinct subsequences of s which equals t.
A string's subsequence is a new string formed from the original string by deleting some (can be none) of the characters without disturbing the remaining characters' relative positions. (i.e., "ACE" is a subsequence of "ABCDE" while "AEC" is not).
The test cases are generated so that the answer fits on a 32-bit signed integer.
- sp1. dp table and index meaning
dp[i][j]: the numbers of [0, j-1] B in [0, i -1 ]A;
- sp2. recurrence formula
if (A[i -1] == B[j - 1]) dp[i][j] =dp[i - 1][j - 1] + dp[i - 1][j]
A : abcc B: abc A[3] == B[2], but A[0]A[1]A[2] = B[0]B[1]B[2], or A[0]A[1]A[3] = B[0]B[1]B[2]
if (A[i -1] != B[j - 1]) dp[i][j] = dp[i - 1][j]
- sp3. initial values
dp[i][0] = 1;
dp[0][j] = 0;
- sp4. literacy directions
3 directions
from left to right, up to down
- sp5. cases
A: "baegg" B: "bag"
B: b a g
1 0 0 0
b 1 1 0 0
a 1 1 1 0
e 1 1 1 0
g 1 1 1 1
g 1 1 1 2
Q.30: Delete Operation for Two Strings
https://leetcode-cn.com/problems/delete-operation-for-two-strings/
Given two strings word1 and word2, return the minimum number of steps required to make word1 and word2 the same.
In one step, you can delete exactly one character in either string.
- sp1. dp table and index meaning
dp[i][j]: the least numbers of deleting characters making [0, j-1] B equals [0, i -1 ]A;
- sp2. recurrence formula
if (A[i -1] == B[j - 1]) dp[i][j] =dp[i - 1][j - 1]
if (A[i -1] != B[j - 1])
- del A[i -1], dp[i][j] = dp[i - 1][j] + 1
- del B[j -1], dp[i][j] = dp[i][j - 1] + 1
- del del A[i -1] && B[j -1], dp[i][j] = dp[i -1][j - 1] + 2
dp[i][j] = min( dp[i - 1][j] + 1, dp[i][j - 1] + 1, dp[i -1][j - 1] + 2)
- sp3. initial values
dp[i][0] = i; (B is empty)
dp[0][j] = j;
- sp4. literacy directions
3 directions
from left to right, up to down
- sp5. cases
A: "sea" B: "eat"
B: e a t
0 1 2 3
s 1 2 3 4
e 2 1 2 3
a 3 2 1 2
Q.31: Edit Distance
https://leetcode-cn.com/problems/edit-distance/
Given two strings word1 and word2, return the minimum number of operations required to convert word1 to word2.
You have the following three operations permitted on a word:
Insert a character
Delete a character
Replace a character
- sp1. dp table and index meaning
dp[i][j]: the least distance of edit characters making [0, j-1] B equals [0, i -1 ]A;
- sp2. recurrence formula
if (A[i -1] == B[j - 1]) dp[i][j] =dp[i - 1][j - 1]
if (A[i -1] != B[j - 1])
- del A[i -1], dp[i][j] = dp[i - 1][j] + 1
- del B[j -1], dp[i][j] = dp[i][j - 1] + 1
- replace A[i -1] && B[j -1], dp[i][j] = dp[i -1][j - 1] + 1
dp[i][j] = min( dp[i - 1][j] + 1, dp[i][j - 1] + 1, dp[i -1][j - 1] + 1)
- sp3. initial values
dp[i][0] = i; (B is empty)
dp[0][j] = j;
- sp4. literacy directions
3 directions
from left to right, up to down
- sp5. cases
A: "horse" B: "ros"
B: r o s
0 1 2 3
h 1 1 2 3
o 2 2 1 2
r 3 2 2 2
s 4 3 3 2
e 5 4 4 3
Q.32: Palindromic Substrings
https://leetcode-cn.com/problems/palindromic-substrings/
Given a string s, return the number of palindromic substrings in it.
A string is a palindrome when it reads the same backward as forward.
A substring is a contiguous sequence of characters within the string.
- sp1. dp table and index meaning
dp[i][j]: substring between [i, j] is Palindromic, then dp[i][j] is true;
- sp2. recurrence formula
if (S[i ] == S[j ])
- if (j - i <= 1) dp[i][j] = true; // a or aa
- if (j - 1 > 1) dp[i + 1][j -1] = true, then… //cabac
if (S[i ] != S[j ]) dp[i][j] = false
- sp3. initial values
dp[i][j] = false
- sp4. literacy directions
3 directions
from left to right, down to up
- sp5. cases
A: "aaa"
1 1 1
0 1 1
0 0 1
Q.33: Palindromic Subsequence
https://leetcode-cn.com/problems/longest-palindromic-subsequence/
Given a string s, find the longest palindromic subsequence's length in s.
A subsequence is a sequence that can be derived from another sequence by deleting some or no elements without changing the order of the remaining elements.
- sp1. dp table and index meaning
dp[i][j]: substring between [i, j] is Palindromic, then dp[i][j] is true;
- sp2. recurrence formula
if (S[i ] == S[j ]) dp[i][j] = dp[i + 1][j -1] + 2;
if (S[i ] != S[j ]) dp[i][j] = max(dp[i + 1][j], dp[i][j -1]);
- sp3. initial values
dp[i][j] = 1 ; if (S[i ] == S[j ]) dp[i][j] = dp[i + 1][j -1] + 2;
dp[i][j] = 0; if (S[i ] != S[j ]) dp[i][j] = max(dp[i + 1][j], dp[i][j -1]);
- sp4. literacy directions
3 directions
from left to right, down to up
- sp5. cases
A: "cbbd"
c b b d
c 1 1 2 2
b 0 1 2 2
b 0 0 1 1
d 0 0 0 1
Q.34: Triangle
https://leetcode-cn.com/problems/longest-palindromic-subsequence/
Given a triangle array, return the minimum path sum from top to bottom.
For each step, you may move to an adjacent number of the row below. More formally, if you are on index i on the current row, you may move to either index i or index i + 1 on the next row.
method top to bottom
- sp1. dp table and index meaning
dp[i][j]: from top to [i, j], the minimum path sum;
- sp2. recurrence formula
dp[i][j] = min(dp[i - 1][j -1], dp[i - 1][j]) + c[i][j];
- sp3. initial values
dp[0][0] = c[i][j]
- sp4. literacy directions
3 directions
up to down
- sp5. cases
dp
2 2
3 4 5
6 5 7 10
4 1 8 3 11
exception:
- The first line: 2, dp[i][0] = dp[i - 1][0] + triangle[i][0];
- The hypotenuse: 2-> 4 -> 7 -> 3 dp[i][j] = dp[i - 1][j -1] + triangle[i][j];
if (triangle == null || triangle.size() == 0) {
return 0;
}
int row = triangle.size();
int column = triangle.get(row - 1).size();
int[][] dp = new int[row][column];
dp[0][0] = triangle.get(0).get(0);
for (int i = 1; i < n; i++) {
dp[i][0] = dp[i - 1][0] + triangle.get(i).get(0);
}
for (int i = 1; i < n; i++) {
int j = 1;
while (j < triangle.get(i).size() - 1) {
dp[i][j] = Math.min(dp[i - 1][j - 1], dp[i - 1][j]) + triangle.get(i).get(j);
j++;
}
dp[i][j] = dp[i - 1][j - 1] + triangle.get(i).get(j);
}
return Arrays.stream(dp[n - 1]).min().getAsInt();
method bottom to top
- sp1. dp table and index meaning
dp[i][j]: from bottom to [0, 0], the minimum path sum;
- sp2. recurrence formula
dp[i][j] = min(dp[i + 1][j -1], dp[i + 1][j]) + c[i][j];
-
sp3. initial values
-
sp4. literacy directions
3 directions
down to up
- sp5. cases
2
3 4
6 5 7
4 1 8 3
dp
2
3 4
6 5 7
4 1 8 3
0 0 0 0 0
dp
2
3 4
7 6 10
4 1 8 3
0 0 0 0 0
2
9 10
7 6 10
4 1 8 3
```java
```java
11
9 10
7 6 10
4 1 8 3
```java
if (triangle == null || triangle.size() == 0) {
return 0;
}
int n = triangle.size();
int[][] dp = new int[n + 1][n + 1];
for (int i = n - 1; i >= 0; i--) {
for (int j = 0; j <= i; j++) {
dp[i][j] = Math.min(dp[i + 1][j + 1], dp[i + 1][j])+ triangle.get(i).get(j);
}
return dp[0][0];
reducing space complexity
2
3 4
6 5 7
4 1 8 3
before:
dp: 0 0 0 0 0 1. dp: 4 1 8 3 0 2. dp: 7 6 10 3 0 3. dp: 9 10 10 3 0 4. dp: 11 10 10 3 0
if (triangle == null || triangle.size() == 0) {
return 0;
}
int row = triangle.size();
int column = triangle.get(row - 1).size();
int[] dp = new int[column + 1];
for (int i = row - 1; i >= 0; i--) {
for (int j = 0; j < triangle.get(i).size(); j++) {
dp[j] = Math.min(dp[j + 1], dp[j])+ triangle.get(i).get(j);
}
return dp[0];
int row = triangle.size();
int[] dp = new int[row + 1];
for (int i = row - 1; i >= 0; i--) {
for (int j = 0; j <= i; j++) {
dp[j] = Math.min(dp[j + 1], dp[j])+ triangle.get(i).get(j);
}
return dp[0];
Q.35: Minimum Falling Path Sum
https://leetcode-cn.com/problems/minimum-falling-path-sum/
Given an n x n array of integers matrix, return the minimum sum of any falling path through matrix.
A falling path starts at any element in the first row and chooses the element in the next row that is either directly below or diagonally left/right. Specifically, the next element from position (row, col) will be (row + 1, col - 1), (row + 1, col), or (row + 1, col + 1).
method top to bottom
- sp1. dp table and index meaning
dp[i][j]: from top to [i, j], the minimum path sum;
- sp2. recurrence formula
dp[i][j] = min(dp[i - 1][j -1], dp[i - 1][j]) + c[i][j];
- sp3. initial values
dp[0][0] = c[i][j]
- sp4. literacy directions
3 directions
up to down
- sp5. cases
dp
2 2
3 4 5
6 5 7 10
4 1 8 3 11
int m = matrix.length;
int n = matrix[0].length;
int[] dp= new int[n + 2];
dp[0] = dp[n + 1] = Integer.MAX_VALUE;
for (int i = m - 1; i >= 0; i--) {
int tmp = 0, last = Integer.MAX_VALUE;
for (int j = 1; j <= n; j++) {
tmp = dp[j];
dp[j] = Math.min(dp[j], Math.min(last, dp[j + 1])) + matrix[i][j - 1];
last = tmp;
}
}
int min = Integer.MAX_VALUE;
for (int j = 1; j <= n; j++) {
min = Math.min(min, dp[j]);
}
return min;
Q.36: Count All Possible Routes
https://leetcode-cn.com/problems/count-all-possible-routes/
You are given an array of distinct positive integers locations where locations[i] represents the position of city i. You are also given integers start, finish and fuel representing the starting city, ending city, and the initial amount of fuel you have, respectively.
At each step, if you are at city i, you can pick any city j such that j != i and 0 <= j < locations.length and move to city j. Moving from city i to city j reduces the amount of fuel you have by |locations[i] - locations[j]|. Please notice that |x| denotes the absolute value of x.
Notice that fuel cannot become negative at any point in time, and that you are allowed to visit any city more than once (including start and finish).
Return the count of all possible routes from start to finish. Since the answer may be too large, return it modulo 109 + 7.
memory search DFS
cache[i][j] cache[i][j]: start form i, before running out of fuel, the path number to reach the target;
int mod = 1000000007;
public int countRoutes(int[] ls, int start, int end, int fuel) {
int n = ls.length;
// initiation
cache = new int[n][fuel + 1];
for (int i = 0; i < n; i++) {
Arrays.fill(cache[i], -1);
}
return dfs(ls, start, end, fuel);
}
int dfs(int[] ls, int u, int end, int fuel) {
// if cache alread has the answer, return
if (cache[u][fuel] != -1) {
return cache[u][fuel];
}
int n = ls.length;
// base case 1:if the fuel is 0,
if (fuel == 0 && u != end) {
cache[u][fuel] = 0;
return 0;
}
// base case 2
boolean hasNext = false;
for (int i = 0; i < n; i++) {
if (i != u) {
int need = Math.abs(ls[u] - ls[i]);
if (fuel >= need) {
hasNext = true;
break;
}
}
}
if (fuel != 0 && !hasNext) {
int a= cache[u][fuel] = u==end?1:0;
return a;
}
int sum = u == end ? 1 : 0;
for (int i = 0; i < n; i++) {
if (i != u) {
int need = Math.abs(ls[i] - ls[u]);
if (fuel >= need) {
sum += dfs(ls, i, end, fuel - need);
sum %= mod;
}
}
}
cache[u][fuel] = sum;
return sum;
}
think about basecase
int mod = 1000000007;
public int countRoutes(int[] ls, int start, int end, int fuel) {
int n = ls.length;
// initiation
cache = new int[n][fuel + 1];
for (int i = 0; i < n; i++) {
Arrays.fill(cache[i], -1);
}
return dfs(ls, start, end, fuel);
}
int dfs(int[] ls, int u, int end, int fuel) {
// if cache alread has the answer, return
if (cache[u][fuel] != -1) {
return cache[u][fuel];
}
int n = ls.length;
int need = Math.abs(ls[u] - ls[end]);
if (need > fuel) {
cache[u][fuel] = 0;
return 0;
}
int sum = u == end ? 1 : 0;
for (int i = 0; i < n; i++) {
if (i != u) {
need = Math.abs(ls[i] - ls[u]);
if (fuel >= need) {
sum += dfs(ls, i, end, fuel - need);
sum %= mod;
}
}
}
cache[u][fuel] = sum;
return sum;
}
from memory search DFS to DP
int dfs(int[] ls, int u, int end, int fuel) {
changable: U and Fuel
dp[i][fuel] = dp[i][fuel] + f[k][fuel - need]
k is the next stop of location i , need is the amount fuel needed from i- k;
int mod = 1000000007;
public int countRoutes(int[] ls, int start, int end, int fuel) {
int n = ls.length;
int[][] dp = new int[n][fuel + 1];
// start = end
for (int i = 0; i <= fuel; i++) {
dp[end][i] = 1;
}
for (int cur = 0; cur <= fuel; cur++) {
for (int i = 0; i < n; i++) {
for (int k= 0; k < n; k++) {
if (i != k) {
int need = Math.abs(ls[i] - ls[u]);
if (cur >= need) {
dp[i][cur] += dp[k][cur - need];
dp[i][cur] %= mod;
}
}
}
}
}
return dp[start][fuel];
}
Q.37: Minimum Falling Path Sum II
https://leetcode-cn.com/problems/minimum-falling-path-sum-ii/
Given an n x n integer matrix grid, return the minimum sum of a falling path with non-zero shifts.
A falling path with non-zero shifts is a choice of exactly one element from each row of grid such that no two elements chosen in adjacent rows are in the same column.
method top to bottom
- sp1. dp table and index meaning
i1: smallest value index i2: the second smallest value index
dp[i][j] = dp[i - 1][i1] + val;
- sp2. recurrence formula
dp[i][j] = (dp[i - 1][i1] || dp[i - 1][j]) + c[i][j];
- sp3. initial values
dp[0][i] = c[0][i]
- sp4. literacy directions
3 directions
up to down
- sp5. cases
1 2 3
4 5 6
7 8 9
i - 1 i1 i2
i i1 i1 i2 i1 i1 i1 i1 i1
//https://programmercarl.com/0070.%E7%88%AC%E6%A5%BC%E6%A2%AF.html#%E5%85%B6%E4%BB%96%E8%AF%AD%E8%A8%80%E7%89%88%E6%9C%AC
