about BinarySearchTree 3
master BST in algo
- Recover Binary Search Tree 99
- Construct Binary Search Tree from Preorder Traversal 1008
- Reconstruct Binary Search Tree With Postorder Traversal
- Reconstruct Binary Search Tree With Level Order Traversal
- Valid Post-order Traversal Of Binary Search Tree
- Count of Range Sum 372
Recover Binary Search Tree 99
Given a Binary Search Tree with only two nodes swapped. Try to find them and recover the binary search tree.
Input:
4
/ \
2 6
/ \ / \
1 5 3 7
Output: 4
/ \
2 6
/ \ / \
1 3 5 7
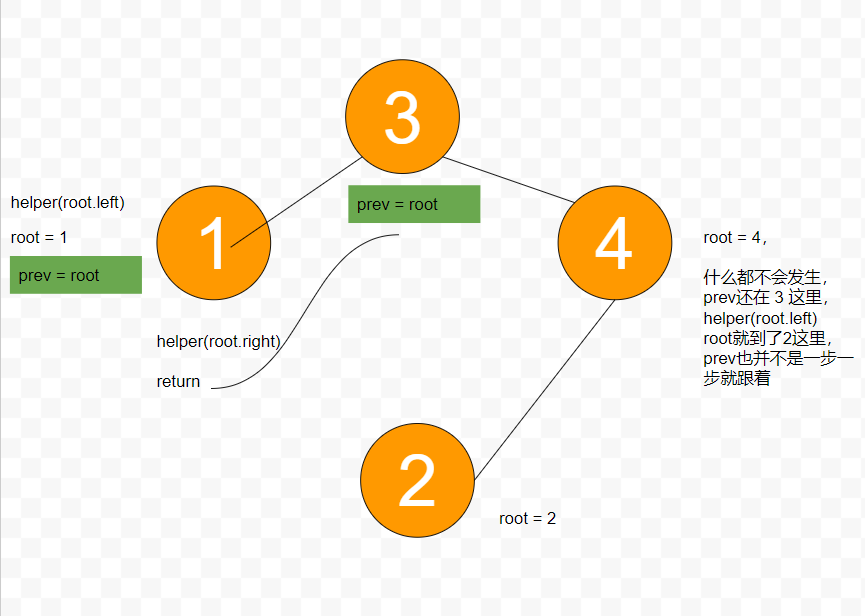
BST
TreeNode prev = null;
TreeNode first = null;
TreeNode second = null;
public TreeNode recover(TreeNode root) {
helper(root);
int tmp = first.key;
first.key = second.key;
second.key = tmp;
return root;
}
private void helper(TreeNode root) {
if( root == null) {
return ;
}
helper(root.left);
if(prev != null) {
if(prev.key > root.key) {
if(first == null) {
first = prev;
}
second = root;
}
}
prev = root;
helper(root.right);
时间复杂度:最坏情况下(即待交换节点为二叉搜索树最右侧的叶子节点)我们需要遍历整棵树,时间复杂度为 O(N)O(N), 其中 NN 为二叉搜索树的节点个数。
空间复杂度:O(H)O(H),其中 HH 为二叉搜索树的高度。中序遍历的时候栈的深度取决于二叉搜索树的高度。
中序遍历有一个特色,比如
. 10
. /
. 5 15
. / \ /
. 3 8 13 16
inOrder: 3 –> 5 -> 8 -> 10 –> 13 –> 15 –> 16
越来越大,这也是 if(prev.key > root.key) 是错误的原因
. 10
. /
. 15 5
. / \ /
. 3 8 13 16
inOrder: 3 –> 15 -> 8 -> 10 –> 13 –> 5 –> 16
. 10
. /
. 3 15
. / \ /
. 5 8 13 16
inOrder: 5 –> 3 -> 8 -> 10 –> 13 –> 5 –> 16
前小后大,就是中序遍历
Construct Binary Search Tree from Preorder Traversal 1008
Given an array of integers preorder, which represents the preorder traversal of a BST (i.e., binary search tree), construct the tree and return its root.
It is guaranteed that there is always possible to find a binary search tree with the given requirements for the given test cases.
A binary search tree is a binary tree where for every node, any descendant of Node.left has a value strictly less than Node.val, and any descendant of Node.right has a value strictly greater than Node.val.
A preorder traversal of a binary tree displays the value of the node first, then traverses Node.left, then traverses Node.right.
Example 1:
Input: preorder = [8,5,1,7,10,12]
Output: [8,5,10,1,7,null,12]
Example 2:
Input: preorder = [1,3]
Output: [1,null,3]
二分法, 无语,二分又混乱了,需要的 return 左边的值,mid 如果压在左边, 用两个值 一大一小,就能发现容易错过,所以压在右边
public TreeNode bstFromPreorder(int[] preorder) {
if (preorder.length == 0) {
return null;
}
return helper(preorder, 0, preorder.length - 1);
}
private TreeNode helper(int[] pre, int start, int end) {
if (start > end) {
return null;
}
TreeNode root = new TreeNode(pre[start]);
if (start == end) {
return root;
}
int i = start, j = end;
while (i < j) {
int mid = i + (j - i + 1) / 2;
if (pre[mid] < pre[start]) {
i = mid ;
} else {
j = mid -1;
}
}
root.left = helper(pre, start + 1, i);
root.right = helper(pre, i + 1, end);
return root;
}
时间: O(N log N), 寻找分界线复杂度是 O(log N)
空间: O (n)
用一个的方式,上标 时间: O(N )
空间: O (n)
这里 i 是 index, 为了避免全局变量
public TreeNode bstFromPreorder(int[] preorder) {
return bstFromPreorder(preorder, Integer.MAX_VALUE, new int[]{0});
}
public TreeNode bstFromPreorder(int[] pre, int bound, int[] i) {
if (i[0] == pre.length || pre[i[0]] > bound) {
return null;
}
TreeNode root = new TreeNode(pre[i[0]++]);
root.left = bstFromPreorder(pre, root.val, i);
root.right = bstFromPreorder(pre, bound, i);
return root;
}
Reconstruct Binary Search Tree With Postorder Traversal
Given the postorder traversal sequence of a binary search tree, reconstruct the original tree.
Assumptions
The given sequence is not null
There are no duplicate keys in the binary search tree
Examples
postorder traversal = {1, 4, 3, 11, 8, 5}
the corresponding binary search tree is
5
/ \
3 8
/ \ \
1 4 11
这两题对比看,上一题是 index 从 0 开始,然后往左边开始,左边需要一个 bound, 那就是 root 值,所以是最大值。
这题是 index 从后面开始,然后右边开始赋值,右边需要一个 bound, 就是 root 值作为它的最小值。
public TreeNode reconstruct(int[] post) {
int len = post.length;
if (len == 0) {
return null;
}
return helper(post, Integer.MIN_VALUE, new int[]{len - 1});
}
private TreeNode helper(int[] post, int min, int[] index) {
if (index[0] < 0 || post[index[0]] <= min) {
return null;
}
TreeNode root = new TreeNode(post[index[0]--]);
root.right = helper(post, root.key, index);
root.left = helper(post, min, index);
return root;
}
Reconstruct Binary Search Tree With Level Order Traversal
Given the levelorder traversal sequence of a binary search tree, reconstruct the original tree.
Assumptions
The given sequence is not null
There are no duplicate keys in the binary search tree
Examples
levelorder traversal = {5, 3, 8, 1, 4, 11}
the corresponding binary search tree is
5
/ \
3 8
/ \ \
1 4 11
public TreeNode reconstruct(int[] level) { // Write your solution here TreeNode root = null; for (int i = 0; i < level.length; i++) { root = helper(root, level[i]); } return root; } private TreeNode helper(TreeNode root, int data) { if (root == null) return new TreeNode(data); if (data <= root.key) root.left = helper(root.left, data); if (data > root.key) root.right = helper(root.right, data); return root; }
其实就是forloop 里面嵌套bst的insert,insert in bst 有iteration 和 recursion 的解法。其中 recursion tree 画出来, 所有node的时间复杂度总和是 o n,n 是bst 的所有node 个数 空间是call stack 最深时所有node 空间复杂度总和,是o h。 所以我写的recursion 和你的 iteration ,时间复杂度一样,空间不用recursion更省啊 ~ An instructor (Paul) endorsed this answer ~
想问一下老师这道题我做的时间复杂度分析,因为每次做一次循环都是从root节点出发去寻找能插进去的位置,是不是就是n*O(height), 然后worst case会不会就是一个糖葫芦串,然后就变成n^2了呢?
Valid Post-order Traversal Of Binary Search Tree
Given an array with integers, determine whether the array contains a valid postorder traversal sequence a BST.
Assumptions:
The given postorder traversal array is not null.
Examples:
For example, a1=[1, 3, 4, 2, 7, 6, 5] is a BST
a2=[1, 3, 4, 6, 7, 2, 5] is not a BST.
Each item in left subtree a[0..i-1] is less than a[n-1]
Each item in right subtree a[i..n-2] is greater than a[n-1]
Both left subtree a[0..i-1] and right subtree a[i..n-2] are BSTs
So, for the given root a[n-1] we can find the start of a potential right subtree by scanning the array from left to right and check where the element is bigger than root. left side of this point is a left subtree. We also need to do sanity check whether the right subtree contains elements greater than root.
{1, 3, 4, 2, 7, 6, 5}
. 5
/
{1, 3, 4, 2} {7, 6} On
/ \
{1} {3, 4} {7} On
/
{3} On
runs in O(ngln) time in average case where the tree is a balanced binary tree and O(n) space. The worst case complexity however is O(n^2) in case of a tall binary tree such as a=[1,2,3,4,5].
我自己是分析 balanced binary tree 空间复杂度是 Oh,但是存疑
public boolean validPostOrder(int[] post) {
if (post.length == 0) {
return true;
}
return helper(post, 0, post.length - 1);
}
private boolean helper(int[] post, int left, int right) {
if (left >= right) {
return true;
}
int root = post[right];
// find left subtree's root, traverse backwards
int leftRoot = right - 1;
while (leftRoot >= left) {
if (post[leftRoot] < root) {
break;
}
leftRoot--;
}
//traver left subtree, if there is an element > root, return false
for (int i = left; i <= leftRoot; i++) {
if (post[i] > root) {
return false;
}
}
return helper(post, left, leftRoot) && helper(post, leftRoot + 1, right -1);
}
用一个 stack, O(n)
其次, 如果是 pre-order of BST, 根据BST 左小右大,则pre order 一路向左下的过程是 decreasing ;那么 post -order ,反过来看则为一路右下为 increasing 。
用 stack 维护 对pre-order linear scan 先 left subtree 的 降序性 , 或者 post -order 反过来 先 right subtree 的 升序性, 从而实现对 given array 的一遍扫描, 时间是O(n) , 也可以处理为 online - algorithm 。
public class Solution {
public boolean validPostOrder(int[] post) {
if (post == null || post.length <= 1) {
return true;
}
return validPostOrder(post, post.length);
// Write your solution here
}
private boolean validPostOrder(int[] post, int n) {
// Creat a stack to maintain increasing order
Deque
// Initialize current root as maximum possible
int root = Integer.MAX_VALUE;
// Traverse post array
for (int i = n - 1; i >= 0; i--) {
// if we find a node who in left subtree and
// larger than root, return false;
if (post[i] > root) {
return false;
}
// If post[i] is in left subtree of stack top,
// Keeping removing items larger than post[i]
// and make the last removed item as the new
// root.
while (!stack.isEmpty() && stack.peek() > post[i]) {
root = stack.peek();
stack.pop();
}
// At this pointer either stack is empty or
// post[i] is larger than root, which is
// increasing order in stack, push post[i]
stack.push(post[i]);
}
return true;
} }
[1, 3, 4, 2, 7, 6, 5]
int i = nums.length; // 7
int max = Integer.MAX_VALUE;
for (int j = nums.length - 1; j >= 0; j--)
{
if (nums[j] > max) return false;
while (i <= nums.length - 1 && nums[j] > nums[i])
max = nums[i++];
nums[--i] = nums[j];
}
return true;
LaiCode 461. Count of Range Sum https://app.laicode.io/app/problem/461
老师好,这道题我的第一想法是类似于max subarray equals to k 的解法,维持一个整体的sum然后把从0开始的partial sum存进map里。由于我们需要求一个范围,我打算用TreeMap,这样看下来TreeMap 的增查应该是O(lgn). 然后submap是O(1),这样看来整体的时间复杂度应该是O(nlogn). 但是由于我们要遍历从upper 到lower的所所有value,这样如果upper 和 lower差的比较大的话 可能最差情况还是O(n), 所以分析下来时间复杂度是O(n^2)对吗
public int countRangeSum(int[] nums, int lower, int upper) { if (nums == null || nums.length == 0) { return 0; } NavigableMap<Long, Integer> map = new TreeMap<>(); map.put(0L, 1); int result = 0; long sum = 0L; for (int i = 0; i < nums.length; i++) { sum += nums[i]; NavigableMap<Long, Integer> subMap = map.subMap(sum - upper, true, sum - lower, true); for (int count : subMap.values()) { result += count; } map.put(sum, map.getOrDefault(sum, 0) + 1); } return result; }
Count of Range Sum 372
Given an integer array nums, return the number of range sums that lie in [lower, upper] inclusive.
Range sum S(i, j) is defined as the sum of the elements in nums between indices i and j (i ≤ j), inclusive.
Note:
A naive algorithm of O(n2) is trivial. You MUST do better than that.
Example:
Given nums = [-2, 5, -1], lower = -2, upper = 2,
Return 3.
The three ranges are : [0, 0], [2, 2], [0, 2] and their respective sums are: -2, -1, 2.
