about BinarySearchTree
master BST in algo
- 前序中序后序
- N-ary Tree Level Order Traversal 429
- Maximum Depth of Binary Tree 104
- <strong>最浅距离的二叉树</strong>
- Count Complete Tree Nodes 222
- Binary Tree Paths 257
- Find Bottom Left Tree Value 513
- Path Sum 112
- Path Sum 113
- Construct Binary Tree from Preorder and Inorder Traversal 105
- Construct Binary Tree from Inorder and Postorder Traversal 106
- insert
前序中序后序
用层序遍历习惯了,今天傻乎乎的不用脑直接用了 Queue, 现在整理下,免得发昏。
首先层序一层层就是先进先出。中序开始是左中右, 夹住了 中间的,所以要用 stack。
-
前序遍历: root,加入右孩子,加入左孩子,这样才能出 root, 左孩子,右孩子, 这里非常重要的是要访问的节点和要加入 list 的节点元素顺序是一致的
-
中序遍历: 左孩子,root, 右孩子。root 先行,不撞左墙不回头,撞了后扔节点,回到它父节点扔了,看看右边有没有小路,有小路不浪费,去右边小路吃了再扔,回到上一个父节点,看看右边还有没有小路吃了扔。
所以这时候会有空栈的问题,到了根部,右边还没开始,需要一个指针来挂住 root,可以往右边走。
这里记得一开始不能做 stack.push(root)。而是进入 while 后 stack.push(cur), 不然是重复计算的。
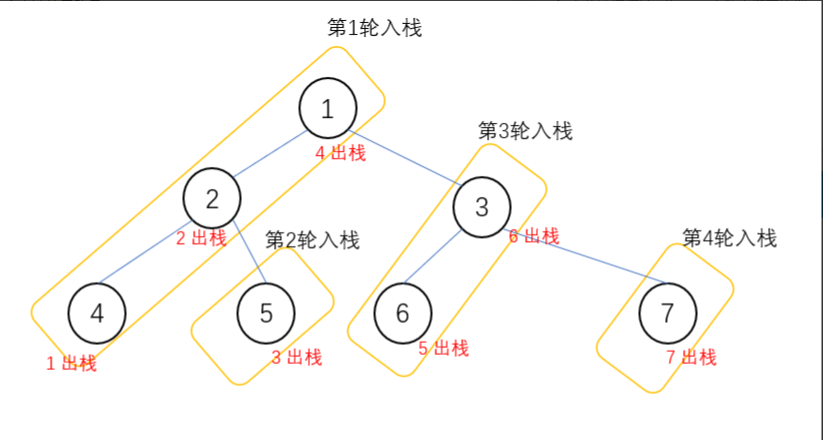
后序遍历
- 后序遍历: 左孩子, 右孩子, root。前序是中左右,所以变成中右左,然后翻转结果,就可以
重点第二个: 到了左墙,扔掉左墙后记录,到了父节点记录,扔出父节点(或者直接用 peek()), 如果发现右边还有吃,重新塞回父节点,后序遍历中没有父亲吃不了右孩子。右边吃完后弹自己,prev = cur, cur = null,这样一步一步往上爬,
. 1
. /
. 2 3
. / \ /
. 4 5 6 7
. /
. 8 9
stack: 1 2 4 8
. 1
. /
. 2 3
. / \ /
. 4 5 6 7
. /
pr 8 9
stack: 1 2 4
list: 8
. 1
. /
. 2 3
. / \ /
.cur 4 5 6 7
. /
pr 8 9
stack: 1 2
list: 8
cur.right != null, 所以 cur 重新入栈, 然后 cur = cur.right
stack: 1 2 4 9
继续执行:pop,9
stack: 1 2 4 list: 8, 9
stack: 1
list: 8, 9 4
cur.right != null, 所以 cur 重新入栈, 然后 cur = cur.right
stack: 1 2
list: 8, 9 4
加入右边:
stack: 1 2 5
list: 8, 9 4
pop
stack: 1
list: 8, 9 4 5 2
继续 cur。right
stack: 1 3
list: 8, 9 4 5 2
另一个方法是加入两个指针,prev 是遍历的上一个指针
Deque<TreeNode> stack = new ArrayDeque<>();
TreeNode cur = root;
TreeNode prev = null; // 前一个访问的节点
while (cur != null || !stack.isEmpty()) {
while (cur != null) {
stack.push(cur);
cur = cur.left; // 中序也是如此
}
cur = stack.pop(), // 出栈
if (cur.right == null || cur.right == prev) { // 从右边返回来,往上的趋势
list.add(cur.val) ; // 弹自己
prev = cur;
cur = null;
} else {
stack.push(cur); //再次压栈
cur = cur.right;
}
}
return list;
}
// 中序
// Deque<TreeNode> stack = new ArrayDeque<>();
// TreeNode cur = root;
// TreeNode prev = null; // 前一个访问的节点
// while (cur != null || !stack.isEmpty()) {
// while (cur != null) {
// stack.push(cur);
// cur = cur.left;
// }
// cur = stack.pop();
// list.add(cur.val);
// cur = cur.right;
// }
// return list;
// }
N-ary Tree Level Order Traversal 429
Given an n-ary tree, return the level order traversal of its nodes' values.
Nary-Tree input serialization is represented in their level order traversal, each group of children is separated by the null value (See examples).
Example 1:
Input: root = [1,null,3,2,4,null,5,6]
Output: [[1],[3,2,4],[5,6]]
我的代码,但是实际上有个小地方要注意
public List<List<Integer>> levelOrder(Node root) {
List<List<Integer>> res = new ArrayList<>();
if (root == null) {
return res;
}
Queue<Node> q = new ArrayDeque<>();
q.offer(root);
while (!q.isEmpty()) {
int size = q.size();
List<Integer> list = new ArrayList<>();
for (int i = 0; i < size; i++) {
Node num = q.poll();
if (num.children != null) {
List<Node> children = num.children;
for (Node n : children) {
q.offer(n);
}
}
list.add(num.val);
}
res.add(list);
}
return res;
}
// if (num.children != null) {
// List<Node> children = num.children;
for (Node n : num.children) {
q.offer(n);
}
这里不需要 check 子类是否为 null, if you see it is 0 at the leaf node, then you can assume that the constructor has initialized it with a empty list instead of null。you don’t normally add a null into a List.
如果是 2 叉树,左右子树,的确需要检查是否为 null
这里比较快的方式是 dfs, 再次了解 input
The height of the n-ary tree is less than or equal to 1000
The total number of nodes is between [0, 104]
In DFS max stack size will be in worst case 1000; in average (well balanced tree) it will be log (height).
in BFS say we have 1 level and all nodes are in that same level i.e. worst case 10 ^ 4 queuing operation (adding 10 ^ 4 elements in dynamic array/queue will have many re-allocate operation
public List<List<Integer>> levelOrder(Node root) {
return levelOrder(root, 0, new ArrayList<>());
}
private List<List<Integer>> levelOrder(Node node, int level, List<List<Integer>> order)
if (node == null) {
return order;
}
List<Integer> list = list.size() > level ? order.get(level) : new ArrayList<>();
list.add(node.val);
if (order.size() <= level) {
order.add(list);
}
for (Node n : node.children) {
levelOrder(n, level + 1, order);
}
return order;
}
}
Maximum Depth of Binary Tree 104
二叉树的最深距离
class Solution {
public int maxDepth(TreeNode root) {
int res = 0;
if (root == null) {
return 0;
}
int left = maxDepth(root.left);
int right = maxDepth(root.right);
return left >= right ? left + 1 : right + 1;
}
}
最浅距离的二叉树
首先距离为根到叶子节点
如果沿用上面的最深的解法,很容易造成结果是 1, 因为左子树是 0, 就变成结果为 0; 但这不符合根到节点的意思
class Solution {
public int maxDepth(TreeNode root) {
int res = 0;
if (root == null) {
return 0;
}
int left = minDepth(root.left);
int right = minDepth(root.right);
// 当左子树为空,右不为空, 这时候不是叶子节点
if (root.left == null) {
return right + 1;
}
// 当右子树为空,左不为空, 这时候不是叶子节点
if (root.right == null) {
return left + 1;
}
// 都不为空才是最小值的深度 + 1
return Math.min(left, right) + 1;
}
}
public int minDepth(TreeNode root) {
if (root == null) {
return 0;
}
Deque<TreeNode> deque = new LinkedList<>();
deque.offer(root);
int depth = 0;
while (!deque.isEmpty()) {
int size = deque.size();
depth++;
for (int i = 0; i < size; i++) {
TreeNode poll = deque.poll();
if (poll.left == null && poll.right == null) {
// 是叶子结点,直接返回depth,因为从上往下遍历,所以该值就是最小值
return depth;
}
if (poll.left != null) {
deque.offer(poll.left);
}
if (poll.right != null) {
deque.offer(poll.right);
}
}
}
return depth;
}
Count Complete Tree Nodes 222
Binary Tree Paths 257
Given the root of a binary tree, return all root-to-leaf paths in any order.
A leaf is a node with no children.
Input: root = [1,2,3,null,5]
Output: ["1->2->5","1->3"]
现在回想 DFS, 吃进去吐出来,我发现一次递归就会有一次回溯。可以看到 dfs 经典题目对应。
这个题目有个 “->” 算两个符号,第一个解法是用 List
public List<String> binaryTreePaths(TreeNode root) {
List<String> res = new ArrayList<>();
if (root == null) {
return res;
}
List<Integer> paths = new ArrayList<>();
traversal(root, paths, res);
return res;
}
private void traversal(TreeNode root, List<Integer> paths, List<String> res) {
paths.add(root.val);
// 叶子结点, 就马上打印,不去 root == null 了
if (root.left == null && root.right == null) {
// 输出
StringBuilder sb = new StringBuilder();
for (int i = 0; i < paths.size() - 1; i++) {
sb.append(paths.get(i)).append("->");
}
sb.append(paths.get(paths.size() - 1));
res.add(sb.toString());
return;
}
// 所以这里就避免 root == null 的情况也属于减枝了,
if (root.left != null) {
traversal(root.left, paths, res);
paths.remove(paths.size() - 1);// 回溯
}
if (root.right != null) {
traversal(root.right, paths, res);
paths.remove(paths.size() - 1);// 回溯
}
}
用 dfs 来的话,经典 dfs 是到了节点的下面, root == null, 一个返回到节点的 dfs root.right, 所以有个反弹力到它的右边,回溯就只有一个。
写了 root == null 这种情况,回溯只需要写一行, 不像上面,因为到叶子节点就 return 了, 所以需要吃了吐,到了右边吃了吐,写两个回溯。
List<String> res = new ArrayList<>();
List<Integer> path = new ArrayList<>();
public List<String> binaryTreePaths(TreeNode root) {
dfs(root);
return res;
}
private void dfs(TreeNode root){
// root 为空
if(root==null) return;
path.add(root.val);
if(root.left==null && root.right==null){
StringBuilder temp = new StringBuilder();
for(int i = 0;i<path.size()-1;i++){
temp.append(path.get(i));
temp.append("->");
}
temp.append(path.get(path.size()-1));
res.add(temp.toString());
}
dfs(root.left);
dfs(root.right);
// 回溯, remove下行来反弹
path.remove(path.size()-1);
}
Find Bottom Left Tree Value 513
Given the root of a binary tree, return the leftmost value in the last row of the tree. Input: root = [2,1,3]
Output: 1
这题没什么好说的,一个 层序遍历到最后,左叶子就是会出现在每层第一个,然后用一个 res 代替, 代替到最后一层。
这题如果是 dfs 做,一开始想到就是把 high 数值一起递归, 我基础较弱会出现想不到全局变量可以直接修改值的情况。
// 两个全局变量
private int value = 0;
private int Hight = -1;
public int findBottomLeftValue(TreeNode root) {
// 一开始递归起始数值
value = root.val;
// 传入 hight来进行对比
helper(root, 0);
// 直接改参数
return value;
}
private void helper(TreeNode root, int hight) {
if (root == null) {
return;
}
if (root.left == null && root.right == null) {
if (hight > Hight) {
Hight = hight;
value = root.val;
}
}
if (root.left != null) {
helper(root.left, hight + 1);
}
if (root.right != null) {
helper(root.right, hight + 1);
}
}
Path Sum 112
Given the root of a binary tree and an integer targetSum, return true if the tree has a root-to-leaf path such that adding up all the values along the path equals targetSum.
A leaf is a node with no children.
Input: root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
Output: true
Explanation: The root-to-leaf path with the target sum is shown.
dfs 左边右边到叶子节点,其中一个满足了就返回。这里又暴露了我的基础知识薄弱. 下面代码中注释的代码是最原始代码,直接两个 dfs, 最后 return false, 因为想着如果进入 dfs 找到了就直接 return true 了, 到弄完了到最后了不就是没找到嘛。
可是直接比如 2 分查找,其实是有循环条件,while,跳出了来个 return false 表示没找到。
public boolean hasPathSum(TreeNode root, int targetSum) {
if (root == null) {
return false;
}
if (root.left == null && root.right == null) {
if (root.val == targetSum) {
return true;
}
// 更优雅的写法
// return root.val == targetSum
}
// hasPathSum(root.left, targetSum - root.val);
// hasPathSum(root.right, targetSum - root.val);
if (hasPathSum(root.left, targetSum - root.val) ){
return true;
};
if (hasPathSum(root.right, targetSum - root.val)) {
return true;
};
return false;
// 更优雅的写法
// return hasPathSum(root.left, targetSum - root.val) || hasPathSum(root.right, targetSum - root.val);
}
Path Sum 113
Given the root of a binary tree and an integer targetSum, return all root-to-leaf paths where the sum of the node values in the path equals targetSum. Each path should be returned as a list of the node values, not node references.
A root-to-leaf path is a path starting from the root and ending at any leaf node. A leaf is a node with no children.
Input: root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
Output: [[5,4,11,2],[5,8,4,5]]
Explanation: There are two paths whose sum equals targetSum:
5 + 4 + 11 + 2 = 22
5 + 8 + 4 + 5 = 22
我显然忘了回溯, 回溯是为了 减少开销,path 上面不需要开辟一个完整的 list, 另外 res.add(new ArrayList<>(path)) 直接用 path 的话,这里是拷贝地址,path数值改变结果会改变
public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
List<List<Integer>> res = new ArrayList<>();
List<Integer> path = new ArrayList<>();
helper(root, targetSum, path, res);
return res;
}
private void helper (TreeNode root, int targetSum, List<Integer> path, List<List<Integer>> res) {
if (root == null) {
return;
}
path.add(root.val);
if (root.left == null && root.right == null) {
if (root.val == targetSum) {
res.add(new ArrayList<>(path));
}
}
helper(root.left,targetSum - root.val, path, res);
helper(root.right, targetSum - root.val, path, res);
path.remove(path.size() - 1);
}
但是用更直白的方式,
public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
List<List<Integer>> res = new ArrayList<>();
// 去掉一个非空
if (root == null) {
return res;
}
List<Integer> path = new ArrayList<>();
helper(root, targetSum, path, res);
return res;
}
private void helper (TreeNode root, int targetSum, List<Integer> path, List<List<Integer>> res) {
path.add(root.val);
if (root.left == null && root.right == null) {
if (root.val == targetSum) {
res.add(new ArrayList<>(path));
}
return; // 到叶子了离开吧,不要往下了
}
// 左边一个递归一个回溯
if (root.left != null) {
helper(root.left,targetSum - root.val, path, res);
path.remove(path.size() - 1);
}
if (root.right != null) {
helper(root.right, targetSum - root.val, path, res);
path.remove(path.size() - 1);
}
}
Construct Binary Tree from Preorder and Inorder Traversal 105
Given two integer arrays preorder and inorder where preorder is the preorder traversal of a binary tree and inorder is the inorder traversal of the same tree, construct and return the binary tree.
Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
Output: [3,9,20,null,null,15,7]
Input: preorder = [-1], inorder = [-1]
Output: [-1]
这题我只切分出了祖先 3 节点, 我也知道 inorder 的 3 的左边是根的左子树,右边是右子树,然后后面就卡了。
但实际上是 inorder 分左右后, preorder 可以继续在这些片区里面的第一个就是根
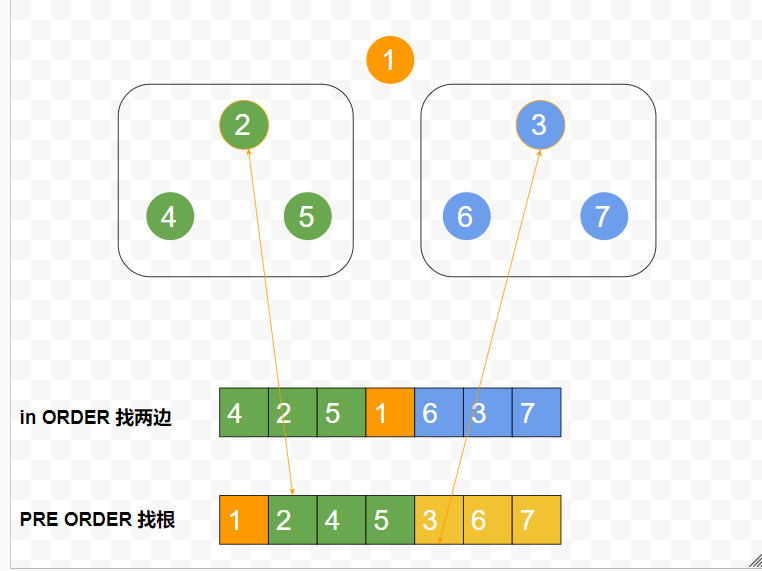
BST
递归三部曲:
- 终止: 当然两个数组为空
- 前序拼出根节点, 两个数组根据这个分成两半; 递归处理这分出来的左边部分, 前序拼出根节点, 两个数组根据这个分成两半, 空了, 递归处理这分出来的右边部分, 前序拼出根节点, 两个数组根据这个分成两半
On 的时间空间复杂度
private Map<Integer, Integer> indexMap;
public TreeNode buildTree(int[] preorder, int[] inorder) {
// 快速定位 inorder的 相对应的 root元素用
int n = preorder.length;
indexMap = new HashMap<>();
for (int i = 0; i < n; i++) {
indexMap.put(inorder[i], i);
}
return helper(preorder, 0, n - 1, inorder, 0, n -1);
}
private TreeNode helper(int[] preorder, int preStart, int preEnd, int[] inorder, int inStar, int inEnd) {
if (preStart > preEnd) {
return null;
}
// preStart找根
int val = preorder[preStart];
TreeNode root = new TreeNode(val);
// 两边的索引要求出来,
// root.left = helper(preorder, ?, ?, inorder, ?, ?);
// root.left = helper(preorder, ?, ?, inorder, ?, ?);
// inorder切两边。所以切点索引要出来
int idx = indexMap.get(val); // 3
// 看看左段数量
int size = idx - inStart; // 1
root.left = helper(preorder, preStart + 1, preStart + size, inorder, inStart, idx - 1);
root.left = helper(preorder, preStart + size + 1, preEnd, inorder, idx + 1, inEnd);
return root;
}
Construct Binary Tree from Inorder and Postorder Traversal 106
这个几乎是一样的思路,再来一次图解找到定位
. Postorder: 4 8 9 5 2 10 6 7 3 1 . ps pe
-
找到 root:idx . root Inorder: 4 2 8 5 9 1 6 10 3 7 . is ie
-
root.left 定位
Inorder: 4 2 8 5 9 1 6 10 3 7 . is idx-1 idx ie
-
左子树距离 : idx - 1 -is
-
postorder 的左子树距离:ps, ps + idx - 1 -is
-
root.right 定位
Inorder: 4 2 8 5 9 1 6 10 3 7 . is idx-1 idx idx + 1 ie
- 右子树距离 : idx + 1, ie
注意这时候 post 最右是 root, 所以递归时候 -1
- postorder 的右子树距离:ps + idx -is, pe -1
insert
iterater
TreeNode insert(TreeNode root, int key) {
if (root == null) {
return new TreeNode(key);
}
TreeNode res = root;
while (root.key != key) {
if (root.key < key) {
if (root.right == null) {
root.right = new TreeNode(key);
}
root = root.right;
} else {
if (root.left == null) {
root.left = new TreeNode(key);
}
root = root.left;
}
}
return res;
}
TreeNode insert(TreeNode root, int key) {
if (root == null) {
return new TreeNode(key);
}
TreeNode res = root;
TreeNode pre = null;
while (root != null) {
pre = root;
if (root.key < key) {
root = root.right;
} else if (root.key > key){
root = root.left;
} else {
return res;
}
} // root == null, 直接挂到 pre上
if (pre.key < key) {
pre.right = new TreeNode(key);
} else if (pre.key > key) {
pre.left = new TreeNode(key);
}
return res;
}
