about BFS 2
master BFS in algo
- Jump Game III 1306
- Check if There is a Valid Path in a Grid 1391
- Reorder Routes to Make All Paths Lead to the City Zero 1466
- Map of Highest Peak 1765
- Path With Minimum Effort 1631
- Count Subtrees With Max Distance Between Cities 1617
Jump Game III 1306
Given an array of non-negative integers arr, you are initially positioned at start index of the array. When you are at index i, you can jump to i + arr[i] or i - arr[i], check if you can reach to any index with value 0.
Notice that you can not jump outside of the array at any time.
Example 1:
Input: arr = [4,2,3,0,3,1,2], start = 5
Output: true
Explanation:
All possible ways to reach at index 3 with value 0 are:
index 5 -> index 4 -> index 1 -> index 3
index 5 -> index 6 -> index 4 -> index 1 -> index 3
用一个 bfs, 和 visited 记录,更快的方式用 dfs
T.C : O(n)
S.C : O(n) [memory used in recursion]
public boolean canReach(int[] arr, int start) {
if (start < 0 || start >= arr.length || arr[start] < 0) {
return false;
} // terminating conditions
if (arr[start] == 0) { //reached the target
return true;
}
arr[start] = -arr[start]; // flip the checked number to negative
return canReach(arr, start + arr[start]) || canReach(arr, start - arr[start]); //checking in both direction
Queue<Integer> q = new ArrayDeque<>();
Set<Integer> set = new HashSet<>();
q.offer(start);
while(!q.isEmpty()){
int tmp = q.poll();
int res = arr[tmp];
if (res == 0) {
return true;
}
if (set.contains(tmp)) {
continue;
}
set.add(tmp);
int x = tmp + arr[tmp];
int y = tmp - arr[tmp];
if (x >= 0 && x < arr.length) {
q.offer(x);
}
if (y >= 0 && y < arr.length) {
q.offer(y);
}
}
return false;
}
Check if There is a Valid Path in a Grid 1391
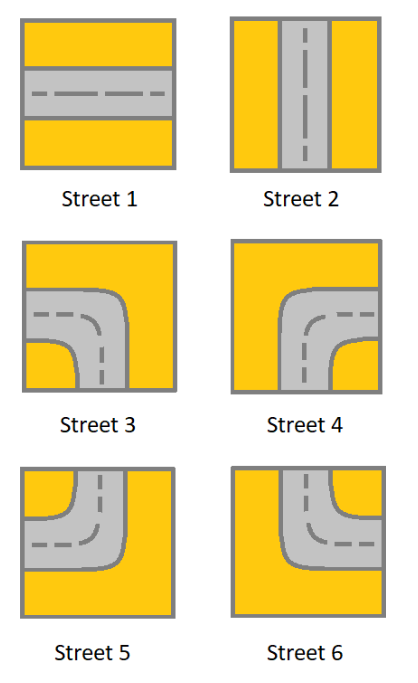
You are given an m x n grid. Each cell of grid represents a street. The street of grid[i][j] can be:
1 which means a street connecting the left cell and the right cell.
2 which means a street connecting the upper cell and the lower cell.
3 which means a street connecting the left cell and the lower cell.
4 which means a street connecting the right cell and the lower cell.
5 which means a street connecting the left cell and the upper cell.
6 which means a street connecting the right cell and the upper cell.
You will initially start at the street of the upper-left cell (0, 0). A valid path in the grid is a path that starts from the upper left cell (0, 0) and ends at the bottom-right cell (m - 1, n - 1). The path should only follow the streets.
Notice that you are not allowed to change any street.
Return true if there is a valid path in the grid or false otherwise.
Example 1:
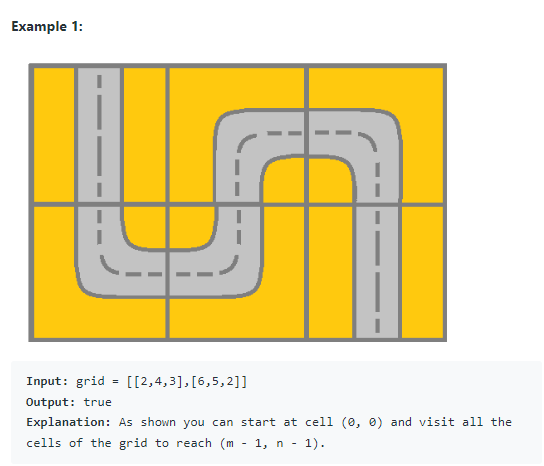
Input: grid = [[2,4,3],[6,5,2]]
Output: true
Explanation: As shown you can start at cell (0, 0) and visit all the cells of the grid to reach (m - 1, n - 1).
BFS
BFS
BFS:
int[][][] dirs = {
// 第一行是 x 坐标,左 -1, 右 1, 第二行是 Y 坐标, 上 -1, 下 1
{{0, -1}, {0, 1}},
{{-1, 0}, {1, 0}},
{{0, -1}, {1, 0}},
{{0, 1}, {1, 0}},
{{0, -1}, {-1, 0}},
{{0, 1}, {-1, 0}}
};
public boolean hasValidPath(int[][] grid) {
int m = grid.length;
int n = grid[0].length;
Queue<int[]> q = new ArrayDeque<>();
boolean[][] visited = new boolean[m][n];
q.offer(new int[]{0, 0});
visited[0][0] = true;
while (!q.isEmpty()) {
int[] cur = q.poll();
int r = cur[0];
int c = cur[1];
// 因为grid是从1 开始
int tmp = grid[r][c] - 1;
for (int[] dir : dirs[tmp]) {
int nr = r + dir[0], nc = c + dir[1];
if (nr < 0 || nr >= m || nc < 0 || nc >= n || visited[nr][nc]) {
continue;
}
// 这个点的四邻遍历
for (int[] backDir : dirs[grid[nr][nc] - 1]) {
if (nr + backDir[0] == r && nc + backDir[1] == c) {
visited[nr][nc] = true;
q.offer(new int[]{nr, nc});
}
}
}
}
return visited[m - 1][n - 1];
}
}
int[][][] dirs = {
// 第一行是 x 坐标,左 -1, 右 1, 第二行是 Y 坐标, 上 -1, 下 1
{{0, -1}, {0, 1}},
{{-1, 0}, {1, 0}},
{{0, -1}, {1, 0}},
{{0, 1}, {1, 0}},
{{0, -1}, {-1, 0}},
{{0, 1}, {-1, 0}}
};
public boolean hasValidPath(int[][] grid) {
int m = grid.length;
int n = grid[0].length;
boolean[][] visited = new boolean[m][n];
return dfs(grid, m, n, 0, 0, visited);
}
boolean dfs(int[][] grid, int m, int n, int r, int c, boolean[][] visited) {
if (r == m - 1 && c == n - 1){
return true;
}
visited[r][c] = true;
for (int[] nextDir : dirs[grid[r][c] - 1]) {
int nr = r + nextDir[0], nc = c + nextDir[1];
if (nr < 0 || nr >= m || nc < 0 || nc >= n || visited[nr][nc]) {
continue;
}
for (int[] backDir : dirs[grid[nr][nc] - 1]) {
if (nr + backDir[0] == r && nc + backDir[1] == c) {
if (dfs(grid, m, n, nr, nc, visited)) {
return true;
}
}
}
}
return false;
}
}
Reorder Routes to Make All Paths Lead to the City Zero 1466
There are n cities numbered from 0 to n - 1 and n - 1 roads such that there is only one way to travel between two different cities (this network form a tree). Last year, The ministry of transport decided to orient the roads in one direction because they are too narrow.
Roads are represented by connections where connections[i] = [ai, bi] represents a road from city ai to city bi.
This year, there will be a big event in the capital (city 0), and many people want to travel to this city.
Your task consists of reorienting some roads such that each city can visit the city 0. Return the minimum number of edges changed.
It's guaranteed that each city can reach city 0 after reorder.
Input: n = 6, connections = [[0,1],[1,3],[2,3],[4,0],[4,5]]
Output: 3
Explanation: Change the direction of edges show in red such that each node can reach the node 0 (capital).
以 0 为根, 往下走,
0
/
4 1
public int minReorder(int n, int[][] connections) {
int count = 0;
Map<Integer, List<Integer>> map = new HashMap<>(); // 每个城市的neibor有多少
Map<Integer, List<Integer>> mapStar = new HashMap<>(); // 每个城市去哪个城市
Queue<Integer> q = new ArrayDeque<>();
for (int[] e: connections) {
// 这里 put 比较块
map.putIfAbsent(e[0], new ArrayList<Integer>());
// map.computerIfAbsent(e[0], k -> new HashSet<>());
map.get(e[0]).add(e[1]);
// map(0, 1, 4), (1, 3, 0), (2, 3), (4, 0), (3, 1, 2)
map.putIfAbsent(e[1], new ArrayList<Integer>());
// map.computerIfAbsent(e[1], k -> new HashSet<>());
map.get(e[1]).add(e[0]);
// [0,1],[1,3],[2,3],[4,0]
mapStar.putIfAbsent(e[0], new ArrayList<Integer>());
// mapStar.computerIfAbsent(e[0], k -> new HashSet<>());
mapStar.get(e[0]).add(e[1]);
}
boolean[] visited = new boolean[n];
q.offer(0);
while (!q.isEmpty()) {
int start = q.poll();
visited[start] = true;
List<Integer> nei = map.get(start);
for (int i : nei) {
if (visited[i] == true) {
continue;
}
q.offer(i);
if (mapStar.containsKey(i) && mapStar.get(i).contains(start)){
continue;
}else {
count++;
}
}
}
return count;
}
Map of Highest Peak 1765
You are given an integer matrix isWater of size m x n that represents a map of land and water cells.
If isWater[i][j] == 0, cell (i, j) is a land cell.
If isWater[i][j] == 1, cell (i, j) is a water cell.
You must assign each cell a height in a way that follows these rules:
The height of each cell must be non-negative.
If the cell is a water cell, its height must be 0.
Any two adjacent cells must have an absolute height difference of at most 1. A cell is adjacent to another cell if the former is directly north, east, south, or west of the latter (i.e., their sides are touching).
Find an assignment of heights such that the maximum height in the matrix is maximized.
Return an integer matrix height of size m x n where height[i][j] is cell (i, j)'s height. If there are multiple solutions, return any of them.
Input: isWater = [[0,1],[0,0]]
Output: [[1,0],[2,1]]
Explanation: The image shows the assigned heights of each cell.
The blue cell is the water cell, and the green cells are the land cells.
int[][] dirs = {
{-1, 0},
{1, 0},
{ 0, -1},
{ 0, 1}
};
public int[][] highestPeak(int[][] isWater) {
Queue<int[]> q = new ArrayDeque<>();
int[][] ans = new int[isWater.length][isWater[0].length];
for (int i = 0; i < isWater.length; i++) {
for (int j = 0; j < isWater[0].length; j++) {
if (isWater[i][j] == 1) {
q.offer(new int[]{i, j});
}
// 没被访问过的陆地起始为-1,水域在答案里要求为0
ans[i][j] = isWater[i][j] == 1 ? 0 : -1;
}
}
while (!q.isEmpty()) {
int[] cur = q.poll();
int x = cur[0], y = cur[1];
for (int[] dir : dirs) {
int nx = x + dir[0];
int ny = y + dir[1];
if (nx < 0 || nx >= isWater.length || ny < 0 || ny >= isWater[0].length || ans[nx][ny] != -1) {
continue;
}
ans[nx][ny] = ans[x][y] + 1;
q.offer(new int[] {nx, ny});
}
}
return ans;
}
Path With Minimum Effort 1631
You are a hiker preparing for an upcoming hike. You are given heights, a 2D array of size rows x columns, where heights[row][col] represents the height of cell (row, col). You are situated in the top-left cell, (0, 0), and you hope to travel to the bottom-right cell, (rows-1, columns-1) (i.e., 0-indexed). You can move up, down, left, or right, and you wish to find a route that requires the minimum effort.
A route's effort is the maximum absolute difference in heights between two consecutive cells of the route.
Return the minimum effort required to travel from the top-left cell to the bottom-right cell.
Example 1:
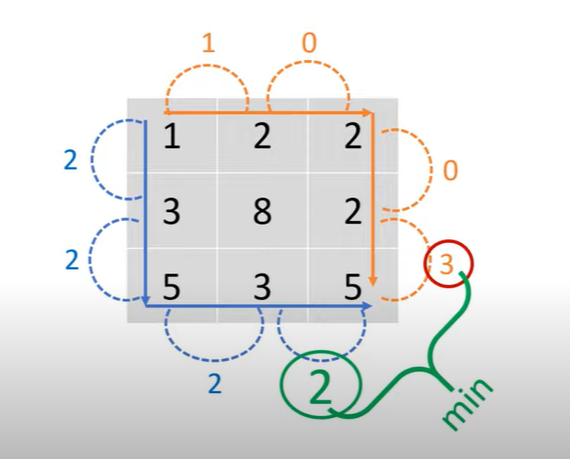
Input: heights = [[1,2,2],[3,8,2],[5,3,5]]
Output: 2
Explanation: The route of [1,3,5,3,5] has a maximum absolute difference of 2 in consecutive cells.
This is better than the route of [1,2,2,2,5], where the maximum absolute difference is 3.
这个算法 Dijikstra, 类型和 BFS 没区别,但是, 它不用 visited 记录. 因为 BFS 每条边权重一样, 利用 for 循环一层一层向外扩散, visited 集合防止走回头路。 而 Dijikstra 是加权图,pq 可能会经过一个节点很多次,找到最少权重的,所以经常会加一个判断,提前 return 来提高效果, 所以创建一个和 input matrix 等长等宽的 matrix, 记录 traverse 到每个坐标花费是多少, 需要一个记录堆 [cost, row, col], 当我们遍历到某个坐标的时候,如果已经记录到 effort 更小时候无需更新,如果重新计算的 newEffort 更小时则需要更新 effort 数组并用这个值带入下一个 BFS 计算
使用优先队列优化的 Dijkstra 算法的时间复杂度为 O(m0log m0), 由于图中的边数为 O(mn),带入即可得到时间复杂度 O(mnlog(mn)。
空间复杂度:O(mn),即为 Dijkstra 算法需要使用的空间。
int[][] dirs = {{-1, 0}, {1, 0},{0, 1},{0, -1}};
public int minimumEffortPath(int[][] heights) {
int m = heights.length;
int n = heights[0].length;
int[][] effort = new int[m][n];
for (int i = 0; i < m; i++) {
Arrays.fill(effort[i], Integer.MAX_VALUE);
}
PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> a[0]-b[0]);
pq.offer(new int[]{0, 0, 0});
while (!pq.isEmpty()) {
int[] min = pq.poll();
int x = min[1], y = min[2], v = min[0];
if (v > effort[x][y]){
continue;
}
if (x == m - 1 && y == n - 1) {
return v;
}
for (int[] dir : dirs) {
int nx = x + dir[0];
int ny = y + dir[1];
if (nx >= 0 && nx < m && ny >= 0 && ny < n ) {
int diff = Math.max(v, Math.abs(heights[nx][ny] - heights[x][y]));
if (diff < effort[nx][ny]) {
effort[nx][ny] = diff;
pq.offer(new int[]{diff, nx, ny});
}
}
}
}
return -1;
}
BFS

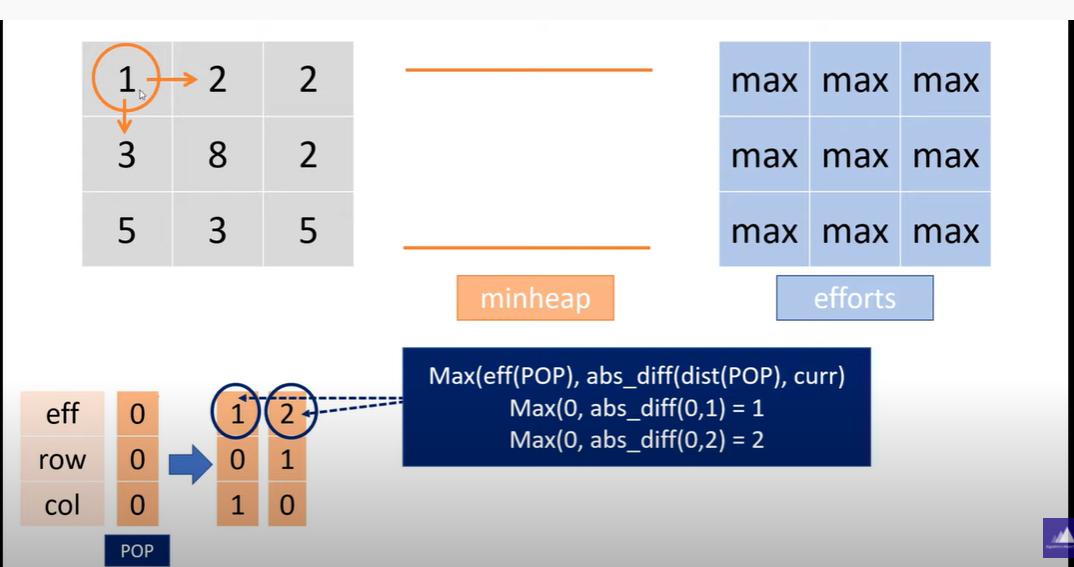
BFS
eff 0 —> 1 2
row 0 —> 0 1
col 0 —> 1 0
pop
BFS
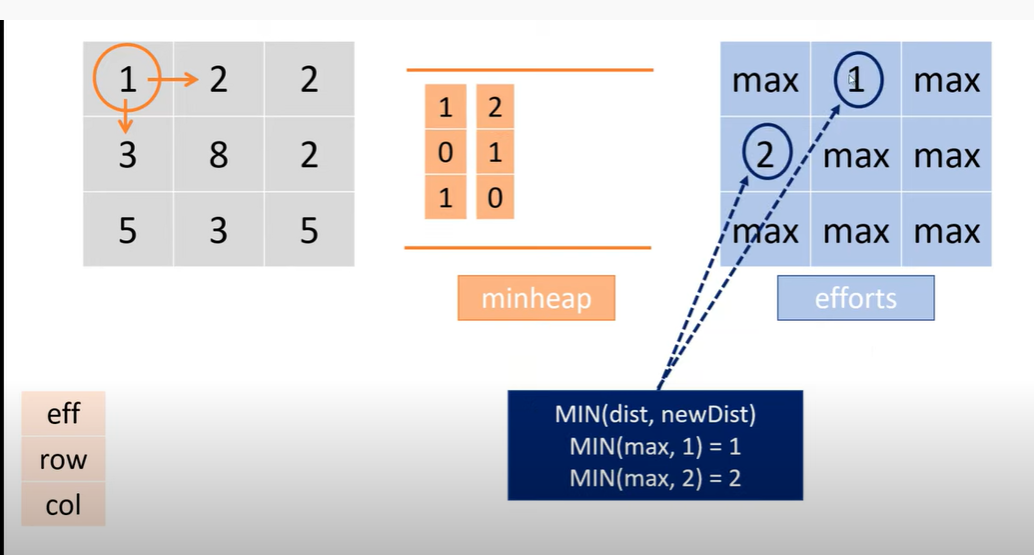
BFS
pop 2, 有 3 个方向, 左,下,右
eff 1 —> 1 6 1
row 0 —> 0 1 0
col 1 —> 2 1 0
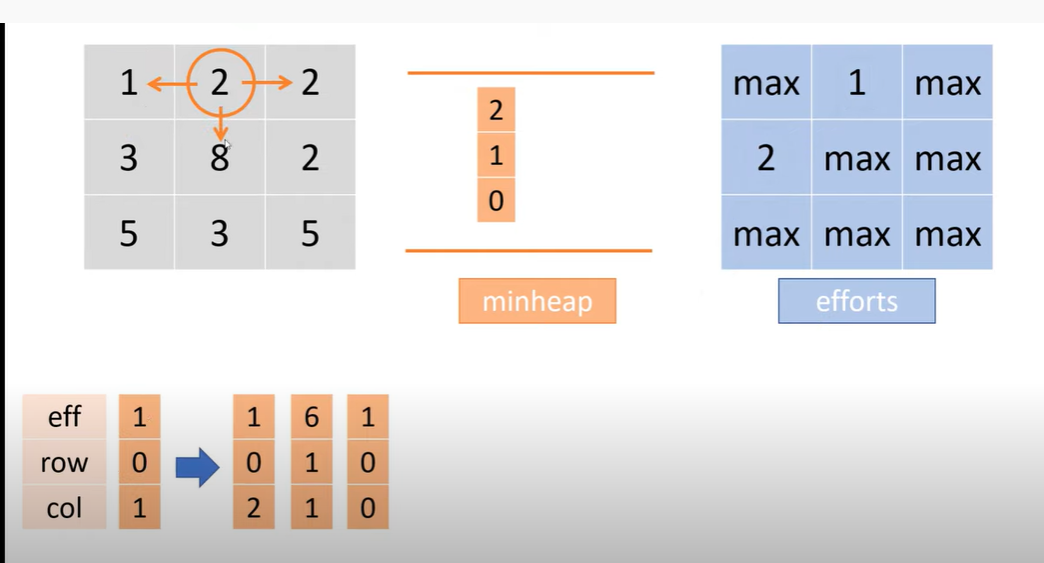
BFS
这里解决了这行代码,取最大值的原因
if (nx >= 0 && nx < m && ny >= 0 && ny < n ) { int diff = Math.max(v, Math.abs(heights[nx][ny] - heights[x][y]));
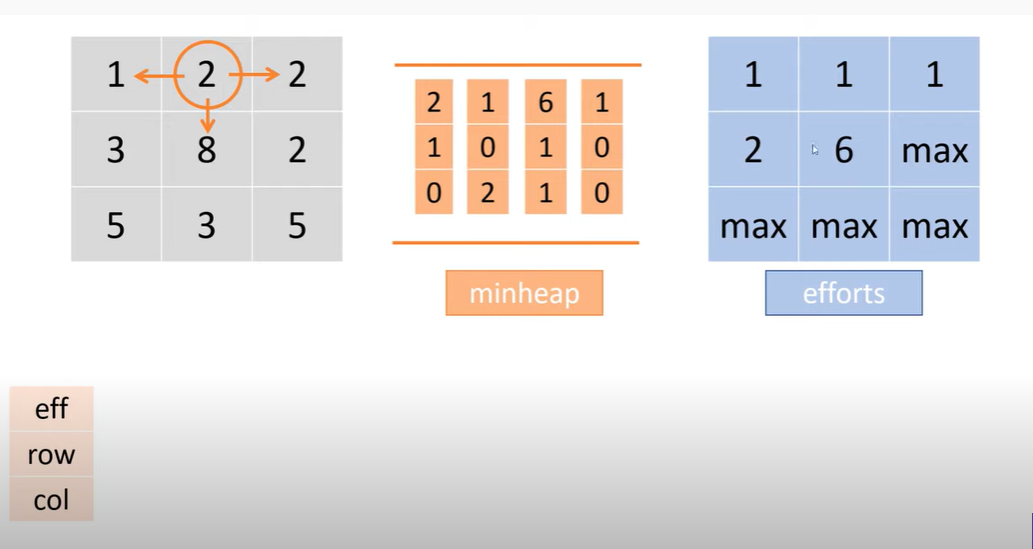
BFS
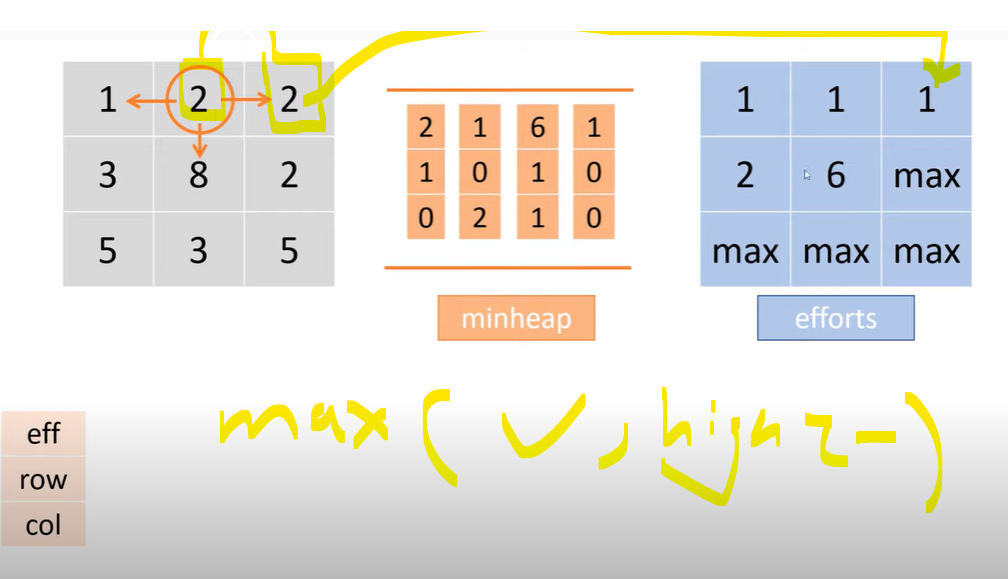
BFS
这时候 minheap 里面有 4 个,effort 表格也有 4 个
pop 右三的 2
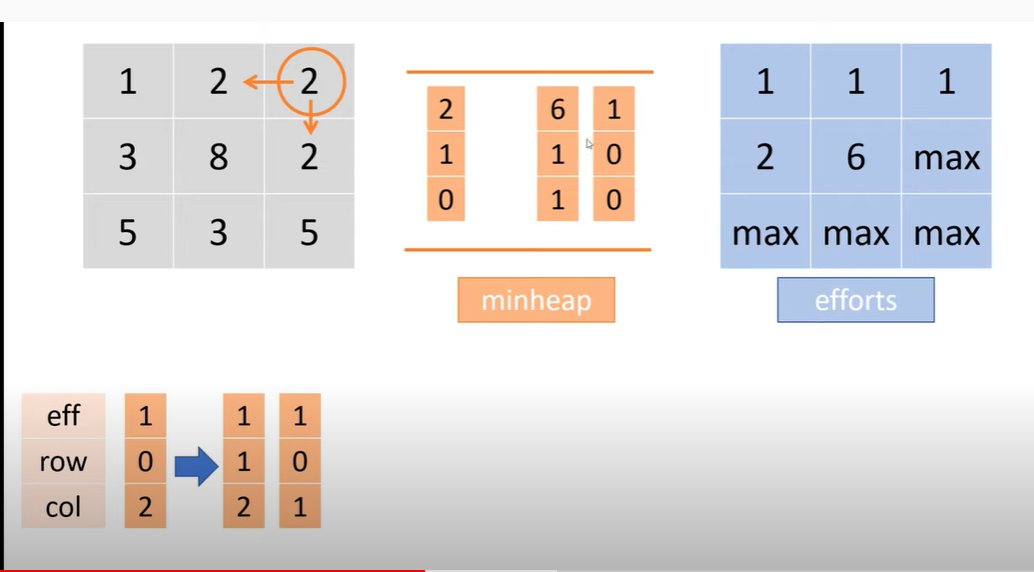
BFS
Count Subtrees With Max Distance Between Cities 1617
There are n cities numbered from 1 to n. You are given an array edges of size n-1, where edges[i] = [ui, vi] represents a bidirectional edge between cities ui and vi. There exists a unique path between each pair of cities. In other words, the cities form a tree.
A subtree is a subset of cities where every city is reachable from every other city in the subset, where the path between each pair passes through only the cities from the subset. Two subtrees are different if there is a city in one subtree that is not present in the other.
For each d from 1 to n-1, find the number of subtrees in which the maximum distance between any two cities in the subtree is equal to d.
Return an array of size n-1 where the dth element (1-indexed) is the number of subtrees in which the maximum distance between any two cities is equal to d.
Notice that the distance between the two cities is the number of edges in the path between them.
Example 1:
Input: n = 4, edges = [[1,2],[2,3],[2,4]]
Output: [3,4,0]
Explanation:
The subtrees with subsets {1,2}, {2,3} and {2,4} have a max distance of 1.
The subtrees with subsets {1,2,3}, {1,2,4}, {2,3,4} and {1,2,3,4} have a max distance of 2.
No subtree has two nodes where the max distance between them is 3.
